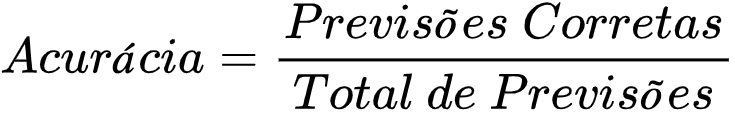Durante o processo de criação de um modelo de machine learning nós precisamos medir a qualidade dele de acordo com o objetivo da tarefa.
Existem funções matemáticas que nos ajudam a avaliar a capacidade de erro e acerto dos nossos modelos, e agora você conhecerá algumas das mais utilizadas.
Neste artigo, usarei a palavra métrica para me referir a essas funções.
Tão importante quanto saber escolher um bom modelo, é saber escolher a métrica correta para decidir qual é o melhor entre eles.
Existem métricas mais simples, outras mais complexas, algumas que funcionam melhor para datasets com determinadas características, ou outras personalizadas de acordo com o objetivo final do modelo.
Ao escolher uma métrica deve-se levar em consideração fatores como a proporção de dados de cada classe no dataset e o objetivo da previsão (probabilidade, binário, ranking, etc). Por isso é importante conhecer bem a métrica que será utilizada, já que isso pode fazer a diferença na prática.
Nenhuma destas funções é melhor do que as outras em todos os casos. É sempre importante levar em consideração a aplicação prática do modelo. O objetivo deste artigo não é ir a fundo em cada uma delas, mas apresentá-las para que você possa pesquisar mais sobre as que achar interessante.
Índice
- Métricas de Classificação em Machine Learning
- Métricas de Regressão em Machine Learning
- Métricas de Ranking em Machine Learning
- Métricas Técnicas vs Métricas de Negócios
Métricas de Classificação em Machine Learning
Estas métricas são utilizadas em tarefas de classificação, e a maioria delas pode ser adaptada tanto para classificação binária quanto de múltiplas classes. Nas tarefas de classificação buscamos prever qual é a categoria a que uma amostra pertence como, por exemplo, determinar se uma mensagem é spam.
Acurácia (Accuracy/Taxa de Acerto)
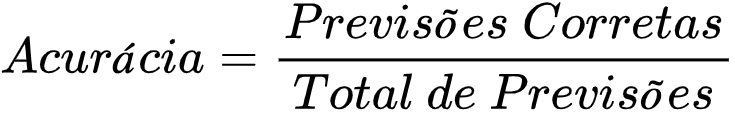
from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred)
Esta é a métrica mais simples.
É o número de acertos (positivos) divido pelo número total de exemplos. Ela deve ser usada em dados com a mesma proporção de exemplos para cada classe, e quando as penalidades de acerto e erro para cada classe forem as mesmas.
Em problemas com classes desproporcionais, ela causa uma falsa impressão de bom desempenho.
Por exemplo, num dataset em que 80% dos exemplos pertençam a uma classe, só de classificar todos os exemplos naquela classe como positivos já se atinge uma precisão de 80%, mesmo que todos os exemplos da outra classe estejam classificados incorretamente.
Leia um artigo detalhado sobre a acurácia em machine learning aqui..
F1 Score
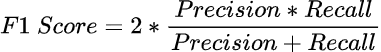
from sklearn.metrics import f1_score
f1_score(y_true, y_pred)
O F1 Score é uma média harmônica entre precisão e recall. Veja abaixo as definições destes dois termos.
Ela é muito boa quando você possui um dataset com classes desproporcionais.
Em geral, quanto maior o F1 score, melhor.
Veja um artigo detalhado sobre o F1 Score aqui.
Precisão (Precision)
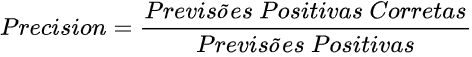
from sklearn.metrics import precision_score
precision_score(y_true, y_pred)
Número de exemplos classificados como pertencentes a uma classe, que realmente são daquela classe (positivos verdadeiros), dividido pela soma entre este número, e o número de exemplos classificados nesta classe, mas que pertencem a outras (falsos positivos).
Veja um artigo detalhado sobre Precisão aqui.
Recall
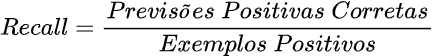
from sklearn.metrics import recall_score
recall_score(y_true, y_pred)
Número de exemplos classificados como pertencentes a uma classe, que realmente são daquela classe, dividido pela quantidade total de exemplos que pertencem a esta classe, mesmo que sejam classificados em outra. No caso binário, positivos verdadeiros divididos por total de positivos.
Veja um artigo detalhado sobre Recall aqui.
ROC AUC - Area Under the ROC Curve
from sklearn.metrics import roc_auc_score
roc_auc_score(y_true, y_pred)
Esta é uma métrica interessante para tarefas com classes desproporcionais. Nela, mede-se a área sob uma curva formada pelo gráfico entre a taxa de exemplos positivos, que realmente são positivos, e a taxa de falsos positivos.
Uma das vantagens em relação ao F1 Score, é que ela mede o desempenho do modelo em vários pontos de corte, não necessariamente atribuindo exemplos com probabilidade maior que 50% para a classe positiva, e menor, para a classe negativa.
Em sistemas que se interessam apenas pela classe, e não pela probabilidade, ela pode ser utilizada para definir o melhor ponto de corte para atribuir uma ou outra classe a um exemplo. Este ponto de corte normalmente é o ponto que se localiza mais à esquerda, e para o alto, no gráfico, mas depende bastante do custo do erro na previsão de uma determinada classe.
Veja um artigo detalhado sobre ROC AUC aqui.
Log Loss
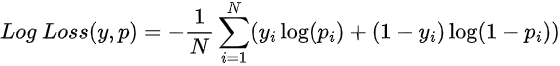
from sklearn.metrics import log_loss
log_loss(y_true, y_pred)
A fórmula do exemplo é para o caso binário, neste caso: p é a probabilidade do exemplo pertencer à classe 1, e y é o valor real da variável dependente.
Esta função pune previsões incorretas muito confiantes. Por exemplo, prever uma classe com uma probabilidade de 95%, e na realidade a correta ser outra.
Ela pode ser utilizada para problemas binários ou com múltiplas classes, mas eu particularmente não gosto de usar em datasets com classes desproporcionais. O valor dela sempre terá a tendência de melhorar se o modelo estiver favorecendo a maior classe presente.
Tomando os cuidados acima, nas situações em que a probabilidade de um exemplo pertencer a uma classe for mais importante do que classificá-lo diretamente, esta função é preferível a usar simplesmente a precisão geral.
Veja um artigo detalhado sobre Log Loss aqui.
Métricas de Regressão em Machine Learning
Nesta parte estão as funções mais comuns utilizadas para avaliar o desempenho de modelos de regressão. Na regressão buscamos prever um valor numérico, como, por exemplo, as vendas de uma empresa para o próximo mês. Nos exemplos abaixo:
Mean Squared Error - MSE
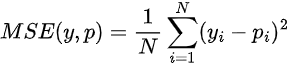
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)
Talvez seja a mais utilizada, esta função calcula a média dos erros do modelo ao quadrado. Ou seja, diferenças menores têm menos importância, enquanto diferenças maiores recebem mais peso.
Existe uma variação, que facilita a interpretação: o Root Mean Squared Error. Ele é simplesmente a raiz quadrada do primeiro. Neste caso, o erro volta a ter as unidades de medida originais da variável dependente.
Basta adicionar o argumento squared=False ao final da função para calcular o RMSE com scikit-learn.
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred, squared=False)
Leia um artigo detalhado sobre RMSE (Raiz do Erro Quadrático Médio) aqui.
Mean Absolute Error - MAE
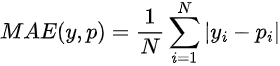
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)
Bastante parecido com MSE, em vez de elevar a diferença entre a previsão do modelo, e o valor real, ao quadrado, ele toma o valor absoluto.
Neste caso, em vez de atribuir um peso de acordo com a magnitude da diferença, ele atribui o mesmo peso a todas as diferenças, de maneira linear.
Se imaginarmos um exemplo simples, onde temos apenas a variável que estamos tentando prever, podemos ver um fato interessante que difere o MSE do MAE, e que devemos levar em conta ao decidir entre os dois: o valor que minimizaria o primeiro erro seria a média, já no segundo caso, a mediana.
Leia um artigo detalhado sobre MAE (Erro Médio Absoluto) aqui.
Mean Absolute Percentage Error - MAPE
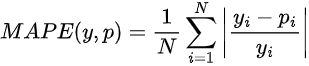
from sklearn.metrics import mean_absolute_percentage_error
mean_absolute_percentage_error(y_true, y_pred)
Este erro calcula a média percentual do desvio absoluto entre as previsões e a realidade.
É utilizado para avaliar sistemas de previsões de vendas e outros sistemas nos quais a diferença percentual seja mais interpretável, ou mais importante, do que os valores absolutos.
Leia um artigo detalhado sobre MAPE (Erro Absoluto Percentual Médio) aqui.
Métricas de Ranking em Machine Learning
Até agora você conheceu a ROC AUC que pode ser usada para medir a qualidade do ranking em casos de classificação binária.
Nesta seção você conhecerá as métricas mais populares para ranking que levam em conta o ordenamento de listas de itens para várias entidades (por exemplo, filmes recomendados a usuários).
Elas são largamente usadas em casos de recomendação.
nDCG - Normalized Discounted Cumulative Gain
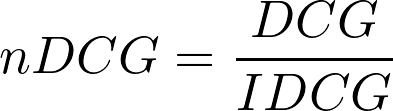
from sklearn.metrics import ndcg_score
ndcg_score(y_true, y_pred)
Esta é a métrica mais interessante para medir a qualidade do ordenamento de uma lista de itens recomendados.
Ela compara os resultados retornados aos usuários pelo modelo (ou qualquer mecanismo de ranking) com os resultados que o usuário teria obtido se tivesse recebido uma lista de itens perfeitamente ordenada.
Temos o DCG (Discounted Cumulative Gain) que é a soma dos ganhos de cada item na lista retornada e o IDCG (Ideal Discounted Cumulative Gain) que é a soma dos ganhos de cada item na lista perfeitamente ordenada de acordo com a relevância real dos itens.
A relevância real dos itens pode ser obtida levando em conta o feedback do usuário, por exemplo, se ele clicou no item ou não.
O nDCG varia entre 0 e 1, onde valores próximos a 1 indicam um bom desempenho e valores próximos a 0 indicam um desempenho ruim.
Leia um artigo detalhado sobre Normalized Discounted Cumulative Gain (NDCG) aqui.
MRR - Mean Reciprocal Rank
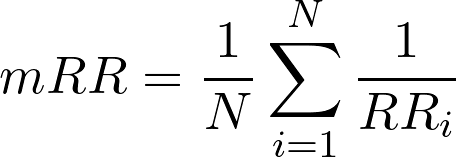
import numpy as np
first_relevant_item_rank = np.array([2, 3, 1, 4])
reciprocal_rank = 1 / first_relevant_item_rank
mrr = reciprocal_rank.mean()
Esta é outra métrica que leva em conta o ordenamento da lista de itens recomendados.
Primeiro devemos calcular o “reciprocal rank”, que é o inverso multiplicativo da posição do primeiro item relevante na lista de itens recomendados.
Depois calculamos a média desses valores considerando o número total de recomendações.
Com um exemplo fica mais fácil de entender. Imagine que essas são as listas de itens recomendados e itens relevantes para 4 usuários:
| Usuário | Itens recomendados | Itens relevantes | Posição do primeiro item relevante | Reciprocal Rank |
|---|---|---|---|---|
| 1 | A, B, C, D, E | B, D | 2 | 1/2 |
| 2 | F, G, H, I, J | H, I | 3 | 1/3 |
| 3 | K, L, M, N, O | K | 1 | 1/1 |
| 4 | P, Q, R, S, T | S | 4 | 1/4 |
Para o usuário 1, o primeiro item relevante aparece na posição 2 da lista de itens recomendados.
Portanto, o “reciprocal rank” para este usuário, nada mais é que 1 sobre o número desta posição, ficando 1/2 = 0,5.
Depois de calcular este “reciprocal rank” para cada usuário, O MRR é então calculado como a média destes valores.
No exemplo acima, o MRR seria de (1/2 + 1/3 + 1/1 + 1/4) / 4 = 0,52.
Novamente, valores próximos a 1 indicam um bom desempenho e valores próximos a 0 indicam um desempenho ruim.
Como ela leva em conta apenas o ranking do item mais relevante, eu prefiro usar o nDCG na maioria dos casos.
Leia um artigo detalhado sobre Mean Reciprocal Rank (MRR) aqui.
MAP - Mean Average Precision
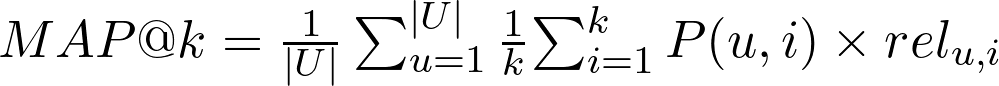
Onde:
- U é o número de usuários (ou listas de resultados)
- k é o número de itens recomendados que devem ser considerados na avaliação
- P(u,i): é a precisão do sistema de recomendação para o item i recomendado para o usuário u
- rel(u,i): é 1 se o item i é relevante para o usuário u e 0 caso contrário
from sklearn.metrics import average_precision_score
average_precision_score(y_true, y_pred)
Mean Average Precision (MAP) é uma métrica mais simples do que o MRR e o NDCG que usa a precisão sobre uma lista de resultados para avaliar modelos de ranking.
Ela mede a proporção de itens relevantes entre os itens retornados pelo modelo para todos os usuários.
Você geralmente a encontra como MAP@k, onde k é o número de itens retornados pelo modelo no topo da lista.
Por exemplo, mesmo que a busca do Google retorne mais de 1000 resultados, o usuário geralmente só vê os primeiros 10 resultados.
Então limitar a lista aos 10 itens mais relevantes e calcular o MAP sobre eles faz mais sentido.
Você deve ter notado que existem duas médias no nome da métrica: “mean” e “average”.
A média referida como “average” é a média da precisão calculada dentro da lista de resultados para cada usuário.
A média referida como “mean” é a média das médias acima, ou seja, a média da precisão média para cada usuário.
A fórmula acima supõe que o número de itens relevantes possíveis para cada usuário é, no mínimo, k. Ou seja, é possível preencher a lista com k itens relevantes.
Leia um artigo detalhado sobre Mean Average Precision (MAP) aqui.
Métricas Técnicas vs Métricas de Negócios
As métricas acima são as mais comuns utilizadas para avaliar o desempenho de modelos durante o desenvolvimento.
Quando o modelo entra em produção, outras métricas se tornam mais importantes. Geralmente são métricas decididas com o time de negócios.
Alguns exemplos são a taxa de cliques em anúncios ou o número de novas vendas atribuídas ao sistema de recomendação.
As métricas técnicas de machine learning correlacionam com métricas de negócio, mas nem sempre uma melhoria nelas significa uma melhoria nas métricas de negócio.
Por isso é importante decidir métricas técnicas para você desenvolver e monitorar o modelo, mas sempre pensar em como elas vão refletir no resultado de negócios esperado.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.