Índice

O Que é RMSE?

A raiz do erro quadrático médio (RMSE ou root mean-square error em inglês) é uma métrica de avaliação amplamente utilizada e reconhecida na comunidade de machine learning para medir o desempenho de modelos de regressão.

Ela é muito útil quando você precisa explicar o desempenho de um modelo para outras pessoas do time, pois elas já estarão acostumadas a trabalhar com essa métrica.

Ela é calculada tomando-se a raiz quadrada da média dos quadrados dos erros, onde o erro bruto é a diferença entre o valor previsto pelo modelo e o valor real.

O RMSE vai muito bem quando você quer que o modelo foque em acertar valores extremos. Ele penaliza erros extremos mais do que erros pequenos.

No entanto, isso torna-o sensível a estes valores extremos, o que pode distorcer a métrica.

Ele é fácil de calcular e requer pouquíssimo código para ser implementado, além de ser fácil de interpretar, já que estima o erro na unidade original do alvo.

Qual a Fórmula do RMSE?

Para calcular o RMSE, basta tirar a raiz quadrada da média dos erros quadrados, conforme a fórmula abaixo:

formula do rmse

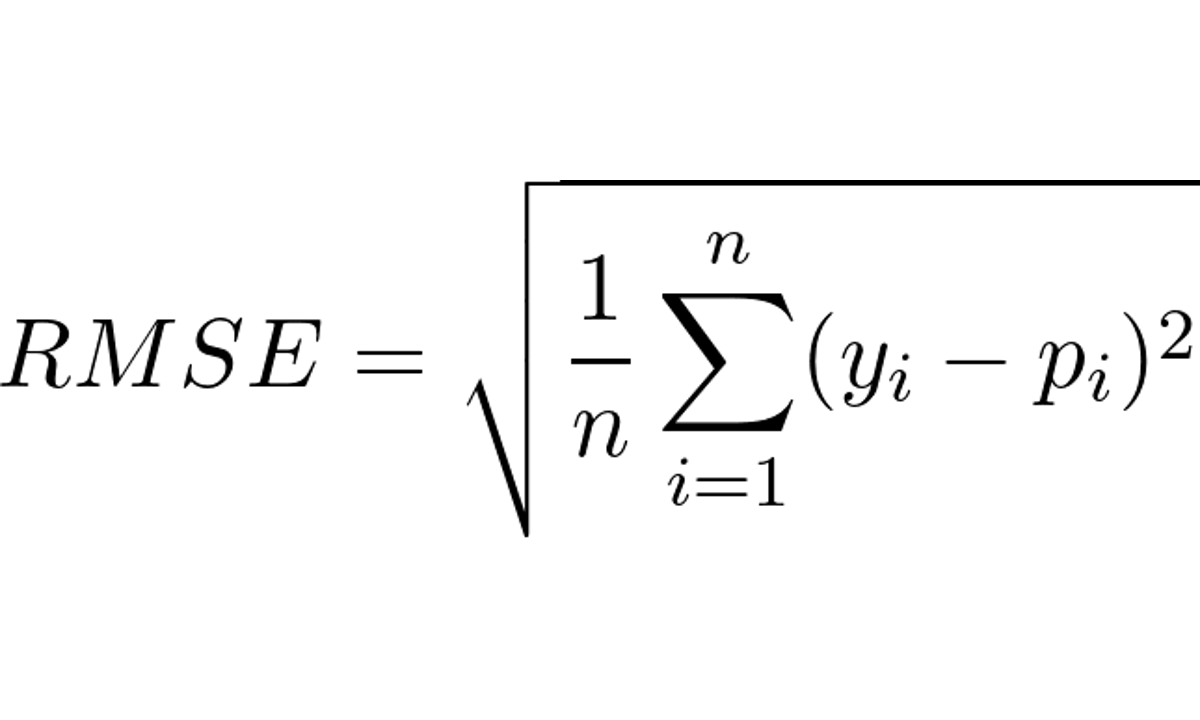
Onde:

  • n é o número de amostras
  • y_i é o valor observado para a amostra i
  • p_i é o valor previsto pelo modelo para a amostra i

Como Interpretar o RMSE?

O RMSE pode ser interpretado como o desvio médio que as previsões têm do alvo.

Por exemplo, imagine que você está construindo um modelo para prever o preço de casas em uma determinada região.

Se o RMSE do seu modelo é de R$ 50.000, isso significa que, em média, o modelo está cometendo um erro de R$ 50.000 em relação aos valores reais.

Na prática, para explicar a tomadores de decisão que não tem background técnico, eu procuro pensar que é a distância média que as previsões estarão do alvo, para cima ou para baixo, similar ao caso do intervalo de confiança.

Mas preste atenção porque isso é diferente de estabelecer um intervalo de confiança para as previsões.

Nunca encontrei alguma prova estatística ou matemática definitiva para te dizer que essa maneira de pensar está rigorosamente correta, mas ela é útil e se aproxima o bastante do que o RMSE está medindo.

Quanto Menor o RMSE Melhor?

Quanto menor o RMSE, melhor o modelo está se saindo.

No entanto, é importante lembrar que o que um RMSE baixo significa pode variar dependendo do contexto.

Um RMSE na casa de 50,000 pode ser ótimo ao tentar prever o preço de um imóvel, mas seria terrível num caso de previsão de temperatura.

Procure estabelecer um número de referência baseado numa solução atual para o problema que você quer resolver ou numa solução simples.

No primeiro caso, calcule o RMSE das estimativas feitas pela solução atual.

No segundo, um exemplo comum é calcular o valor médio do alvo nos dados de treino e calcular o RMSE usando este valor como previsão.

Seu modelo precisa ter um RMSE menor do que esse para justificar seu uso, já que não faz sentido usar um modelo que não é capaz de errar menos que uma solução simples como essa.

Como Calcular o RMSE Usando Scikit-learn em Python?

Calcular o RMSE é muito simples e você pode criar sua própria função facilmente.

Mas para evitar erros num dia em que você estiver cansado, eu recomendo que você use a função mean_squared_error do módulo metrics do scikit-learn com o argumento squared=False.

from sklearn.metrics import mean_squared_error

# Valores reais do alvo
y_true = [200, 180, 220]

# Valores previstos pelo modelo
y_pred = [190, 180, 210]

# Calcula o MSE
rmse = mean_squared_error(y_true, y_pred, squared=False)

print(rmse)

A função mean_squared_error recebe os argumentos y_true (os valores reais do alvo) e y_pred (os valores previstos pelo modelo) como parâmetros.

Os argumentos podem ser listas do Python, arrays do Numpy ou até Series do pandas.

Se você não adicionar o argumento squared=False, ele retorna o MSE, pois o valor padrão deste argumento é squared=True, já que a função leva o nome da métrica sem a transformação da raiz.

Como Calcular o RMSE em R?

A mesma ideia se aplica à linguagem R. Dá pra calcular do zero, mas vamos usar a função rmse da biblioteca Metrics para evitar erros.

library(Metrics)

# Valores reais do alvo
y_true <- c(200, 180, 220)

# Valores previstos pelo modelo
y_pred <- c(190, 180, 210)

# Calcula o RMSE
rmse <- rmse(y_true, y_pred)

print(rmse)

Assim como no scikit-learn, a função recebe os argumentos y_true com os valores reais do alvo e y_pred com as previsões do modelo.

Por ser uma função específica para o RMSE, não precisamos de argumentos adicionais.

Diferença Entre RMSE e MSE

MSE é o Erro Quadrático Médio.

A principal diferença entre elas é que o RMSE é a raiz quadrada da média dos erros ao quadrado, enquanto o MSE é a própria média dos erros ao quadrado.

Em geral, o RMSE é mais comumente utilizado na avaliação do modelo em dados fora da amostra, pois ele fornece uma medida mais intuitiva, já que os resultados são expressos nas unidades de medida originais dos dados observados.

O MSE é largamente utilizado internamente como função objetivo para treinar o modelo, já que aí não há a necessidade de se preocupar com a interpretação das unidades do erro e é mais fácil de calcular o gradiente.

Diferença Entre RMSE e MAE

MAE é o Erro Médio Absoluto.

A principal diferença entre estas métricas é que o RMSE é mais sensível às observações com erros muito grandes, enquanto o MAE é mais “robusto” a outliers (observações com valores muito distantes da maioria das outras observações).

Considere um conjunto de dados com 10 observações, onde 9 dessas observações têm um erro bruto de 1 e uma observação tem um erro bruto de 100.

Se você estiver usando o RMSE como métrica de avaliação, o erro bruto de 100 será elevado ao quadrado e terá uma influência muito maior no resultado final do que os erros de 1.

No entanto, se você estiver usando o MAE como métrica de avaliação, o erro bruto de 100 continuará com o mesmo valor e não afetará tão gravemente o resultado final.

Então, se você tiver um conjunto de dados com outliers e quiser minimizar a influência desses pontos no modelo, pode ser uma boa ideia optar pelo MAE.

Diferença Entre RMSE e MAPE

O MAPE é o Erro Médio Percentual Absoluto.

A diferença principal entre essas métricas é que o RMSE é uma medida do erro nas unidades originais, enquanto o MAPE é uma medida relativa do erro, sempre retornando o erro em valores percentuais.

A segunda diferença importante é que o RMSE eleva o erro ao quadrado, enquanto o MAPE usa o valor absoluto, similar ao MAE.

O caso de uso em que eu mais vejo preferência pelo MAPE sobre o RMSE é a previsão de demanda de produtos.

Nestes casos, o erro relativo é muito mais informativo e fácil de interpretar.

Por exemplo, prever que um produto venderá 9.950 unidades quando o valor real de vendas for 10.000 unidades é menos problemático do que prever que ele venderá 50 unidades e na verdade o produto vender 100.

Nesse caso, o MAPE é uma métrica mais adequada, pois vai te dar um erro maior para o caso mais problemático.

O RMSE, por outro lado, emitirá o mesmo erro para os dois casos.

Diferença Entre RMSE e R-quadrado

R-quadrado estima quão bem o modelo explica a variação nos valores observados.

Ele é um valor entre 0 e 1, onde um valor próximo de 1 indica que o modelo explica bem os dados observados.

É raro ver R-quadrado sendo usado na prática de machine learning fora de ambientes acadêmicos com foco forte em estatística tradicional.

Apesar de popular na academia, existem vários problemas com esta métrica, que foram muito bem expostos pelo professor Cosma Shalizi da Universidade Carnegie Mellon.

Dentre as alegações contra o R-quadrado estão que ele não mede o ajuste do modelo de forma confiável e não diz nada sobre o erro de previsão

Ele pode ser arbitrariamente baixo mesmo quando o modelo está completamente correto ou arbitrariamente próximo de 1 mesmo quando o modelo está totalmente errado.

Você pode ver as alegações completas sobre os problemas com R-quadrado, com justificativas, neste artigo em inglês.

Baseado nisso, eu recomendo que você só use o R-quadrado se seu chefe ou professor exigir.

Como o RMSE é Afetado Por Outliers?

Outliers são valores extremos que estão fora da faixa normal de um conjunto de dados.

Eles podem ter um impacto significativo no modelo, pois podem distorcer a média e, consequentemente, afetar o valor do RMSE.

Por exemplo, imagine novamente que temos um conjunto de dados de preço de casas em uma cidade.

Se tivermos 4 casas com valor de R$ 100.000 e uma casa com valor de R$ 2.000.000, esta última pode ter uma influência muito maior no RMSE.

Isso pode ser ilustrado da seguinte maneira (dividi os valores por 1.000 para não ficar confuso com tantos zeros):

Valor observado Valor previsto pelo modelo Erro quadrado
100 90 100
100 95 25
100 95 25
100 95 25
2000 1000 1000000 
RMSE = raiz quadrada de (soma dos erros quadrados / número de observações)
RMSE = raiz quadrada de (1000175 / 5)
RMSE = raiz quadrada de 200035
RMSE = 447,25

Se excluirmos a casa mais cara:

RMSE = raiz quadrada de (175 / 4)
RMSE = raiz quadrada de 43,75
RMSE = 6,61

Nem sempre é correto excluir os outliers, então recomendo que você avalie seu modelo com mais métricas além do RMSE para ter uma perspectiva melhor de como ele está atuando em várias áreas dos seus dados (por exemplo, valores extremos vs valores médios).

O RMSE Pode Ser Usado Para Avaliar Modelos De Classificação?

Eu não recomendo que você use RMSE para avaliar modelos de classificação, já que ele foi criado pensando em rótulos puramente numéricos em vez de categorias ou classes.

Dito isso, existe uma métrica chamada Brier Score que é basicamente o erro quadrático médio (sem a raiz) aplicada a casos de classificação binária

A fórmula para o Brier Score é dada por:

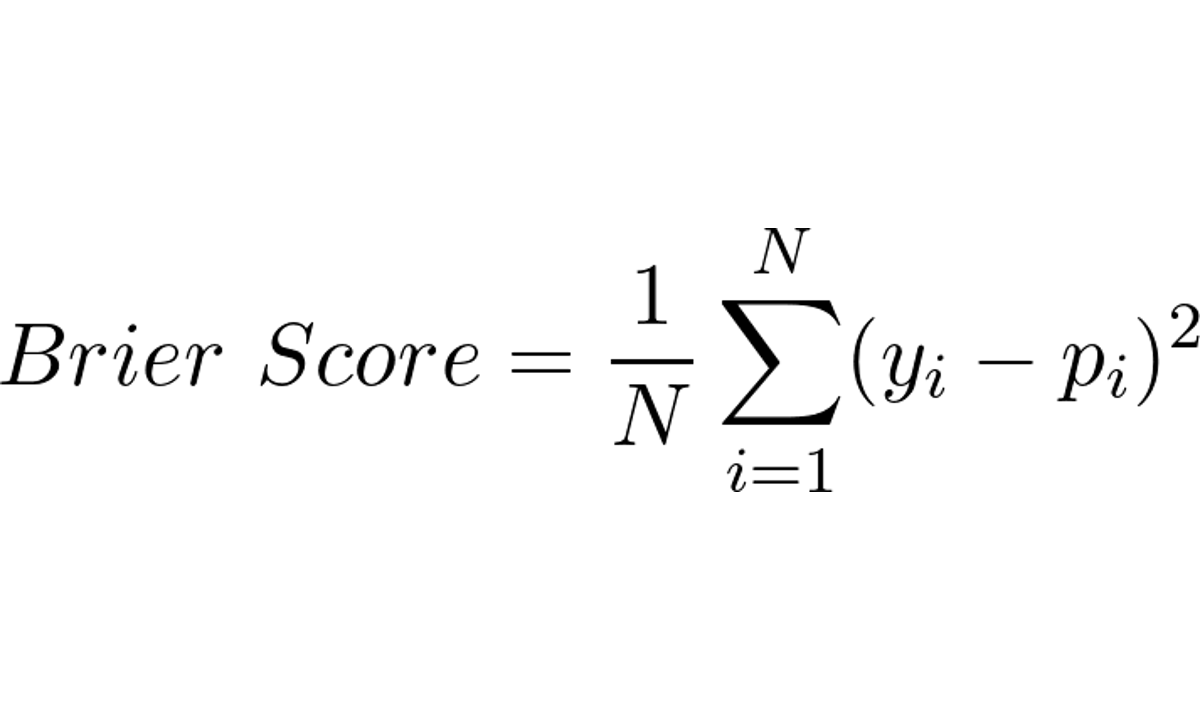
formula do brier score

Onde:

  • N é o número de exemplos no conjunto de dados
  • p_i é a probabilidade prevista pelo modelo do evento ocorrer na amostra i
  • y_i é o valor real (0 ou 1) indicando se o evento ocorreu na amostra i

Ele varia entre 0 e 1, sendo 0 o melhor possível e 1 o pior possível, ou seja, quanto menor o Brier Score, melhor o desempenho do modelo.

Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.
Coursera banner