De todos os tipos de previsão, prever o que ocorrerá no futuro com base em eventos passados pode ser uma das tarefas mais interessantes e desafiadoras.
É aí que entra a previsão de séries temporais.
Prever uma série temporal começa por supor que os padrões de comportamento observados no passado serão replicados no futuro.
Uma das maneiras de fazer estas previsões é usando modelos estatísticos sobre séries univariadas, que é o que você vai aprender neste artigo usando Python.
Séries univariadas são aquelas em que usamos apenas a variável dependente (nosso alvo) para fazer previsões.
Vamos utilizar a biblioteca statsforecast que tem crescido bastante nos últimos meses.
Ela reúne os modelos estatísticos de previsão de séries temporais mais populares numa interface simples, nos permitindo fazer previsões probabilísticas e de ponto.
Além disso, você não fica limitado a prever uma série de cada vez, ela é feita para ser escalável para prever múltiplas séries ao mesmo tempo.
Isso é comum, já que geralmente temos séries temporais de vários locais, produtos, etc.
Índice
- Qual a Diferença Entre Previsão Probabilística e Previsão de Ponto?
- Como Carregar e Processar Os Dados Para Previsão de Séries Temporais
- Como Instalar o Statsforecast?
- Como Saber Se o Modelo Está Bom?
- Baseline Simples Do Último Valor
- ARIMA
- Suavização Exponencial (Exponential Smoothing)
- Treinando Vários Modelos de Séries Temporais Ao Mesmo Tempo
Qual a Diferença Entre Previsão Probabilística e Previsão de Ponto?
A previsão probabilística nos dá um intervalo de valores para o que estamos tentando prever.
Por exemplo, em vez de cravar que a temperatura de amanhã será de 30 graus, podemos dizer que existe 90% de chance que a temperatura de amanhã esteja entre 28 e 32 graus.
Rigorosamente falando, o intervalo de valores que cobre 90% quer dizer que a probabilidade de que a temperatura de amanhã esteja dentro deste intervalo é de 90%.
Já no caso da previsão de ponto, estamos cravando o resultado, dando apenas o valor mais provável da temperatura.
A previsão probabilística é preferível, porque reflete melhor a incerteza quando fazemos previsões.
Na previsão de ponto nós não sabemos qual a confiança do modelo naquele valor específico.
Pense numa previsão em que o ponto mais provável é 30 graus, mas o intervalo de valores que cobre 90% é de 28 a 32 graus, comparada a outra em que o intervalo de valores que cobre 90% é de 25 a 35 graus.
Apesar do ponto mais provável ser o mesmo, nosso modelo tem mais confiança na primeira previsão, já que o intervalo que cobre 90% dos valores é menor.
Por outro lado, a previsão de ponto é mais simples e fácil de entender.
Como Carregar e Processar Os Dados Para Previsão de Séries Temporais
Vamos usar algumas séries simples univariadas para demonstrar como usar a biblioteca statsforecast.
As técnicas que você aprenderá aqui servem para qualquer área, mas como a maior parte dos casos de consultoria de previsão de séries temporais que faço envolvem previsão de demanda, vamos usar um conjunto de dados de vendas de uma loja de varejo.
Estes são dados diários reais de produtos vendidos numa rede de lojas chamada Favorita no Equador.
Vamos carregar os dados usando pandas e dividir em treino e validação.
Nossa validação será uma divisão temporal simples, onde 3 meses de vendas serão usados para avaliar os modelos fora da amostra de treino.
Assim também poderemos comparar quais métodos funcionam melhor.
Lembre-se que um método ser o melhor para este conjunto de dados não significa que ele será o melhor para o seu caso.
O mais importante aqui é você aprender a rodar vários modelos e comparar os resultados.
import pandas as pd
import numpy as np
data = pd.read_csv('train.csv', index_col='id', parse_dates=['date'])
O conjunto de dados contém vendas diárias de 33 categorias de produtos em 54 lojas entre 2013 e 2017.
| id | date | store_nbr | family | sales | onpromotion |
|---|---|---|---|---|---|
| 752075 | 2014-02-28 00:00:00 | 11 | BREAD/BAKERY | 450 | 0 |
| 2517272 | 2016-11-16 00:00:00 | 39 | SEAFOOD | 8 | 1 |
| 2540112 | 2016-11-29 00:00:00 | 30 | BEVERAGES | 1422 | 40 |
| 2379367 | 2016-08-31 00:00:00 | 20 | BABY CARE | 1 | 0 |
| 700715 | 2014-01-30 00:00:00 | 2 | PET SUPPLIES | 8 | 0 |
Onde:
- “id” é um identificador único para cada registro na tabela.
- “date” é a data em que as vendas foram registradas.
- “store_nbr” é o identificador da loja onde as vendas aconteceram.
- “family” é a categoria dos produtos vendidos.
- “sales” é a quantidade de unidades vendidas (o alvo de nossa previsão).
- “onpromotion” é a quantidade de produtos daquela categoria que estavam em promoção naquele dia
Para simplificar a análise, vamos selecionar apenas as vendas de uma das lojas, mas vamos manter todas as categorias de produtos.
Por ser um tutorial sobre métodos univariados, vamos usar apenas as colunas “date”, “family” e “sales”.
Apesar delas estarem empilhadas no mesmo DataFrame, temos 33 séries temporais univariadas, uma para cada categoria de produto.
Você pode prever todas as categorias para todas as lojas, mas como estamos aprendendo, vamos com calma.
Para usar o statsforecast, precisamos passar os dados com 3 colunas:
ds: data da observaçãoy: valor que queremos preverunique_id: identificador da série (categoria dos produtos no nosso caso)
data2 = data.loc[data['store_nbr'] == 1, ['date', 'family', 'sales']]
data2 = data2.rename(columns={'date': 'ds', 'sales': 'y', 'family': 'unique_id'})
Esse código seleciona apenas as linhas da tabela data referentes à loja 1 e as colunas “date”, “family” e “sales”. Isso é feito usando a função loc do pandas para evitar aquele monte de warnings que ele dá quando você tenta acessar colunas usando o operador de colchetes.
Depois usamos a função rename do pandas passando um dicionário para o argumento columns para renomear as colunas da tabela resultante data2 para o formato esperado pelo statsforecast.
As colunas “date”, “sales” e “family” tornam-se “ds”, “y” e “unique_id” respectivamente.
A nova tabela tem esse formato:
| id | ds | unique_id | y |
|---|---|---|---|
| 0 | 2013-01-01 00:00:00 | AUTOMOTIVE | 0 |
| 1 | 2013-01-01 00:00:00 | BABY CARE | 0 |
| 2 | 2013-01-01 00:00:00 | BEAUTY | 0 |
| 3 | 2013-01-01 00:00:00 | BEVERAGES | 0 |
| 4 | 2013-01-01 00:00:00 | BOOKS | 0 |
O “id” é o índice do dataframe, que será ignorado pelo statsforecast.
Vamos separar os dados do ano inteiro de 2013 para treino e os 3 primeiros meses de 2014 para validação.
train = data2.loc[data2['ds'] < '2014-01-01']
valid = data2.loc[(data2['ds'] >= '2014-01-01') & (data2['ds'] < '2014-04-01')]
h = valid['ds'].nunique()
h é o horizonte: o número de períodos que queremos prever. Neste caso, é o número de datas únicas no conjunto de validação (aproximadamente 90 dias).
Dificilmente você usará um modelo para prever um ano inteiro porque a qualidade das previsões vai cair muito depois de um tempo, por isso selecionei apenas 3 meses para validação.
Por outro lado, é importante usar um conjunto de dados de treino que inclua períodos de alta e baixa sazonalidade, para que o modelo aprenda a lidar com essas situações.
Com isso pronto, vamos começar a modelagem.
Como Instalar o Statsforecast?
A forma mais simples de instalar o statsforecast é usando o pip:
pip install statsforecast
ou conda:
conda install -c conda-forge statsforecast
Lembre-se de criar um ambiente virtual para não ter problemas com seu ambiente de trabalho!
Como Saber Se o Modelo Está Bom?
Precisamos de uma métrica e um valor de referência para comparar os resultados dos modelos.
A melhor maneira de escolher o valor de referência é calculando a métrica de avaliação escolhida sobre uma solução que seja usada atualmente, como por exemplo o sistema atual de previsão de vendas da empresa.
Caso não tenha como fazer essa medição, ou não exista um sistema atual, você pode usar soluções triviais como as que vou mostrar a seguir.
Elas são chamadas de “baseline”, porque são o valor mínimo que nosso modelo deve superar para justificar o uso dele em produção.
Afinal, se um modelo mais complexo não for capaz de superar uma solução trivial, o custo-benefício da implementação não compensa.
Vamos utilizar a métrica wMAPE (Weighted Mean Absolute Percentage Error ou Erro Absoluto Percentual Médio Ponderado) para avaliar os modelos.
Esta é uma variação do MAPE, uma métrica muito utilizada por ser simples de entender (facilita na hora de explicar para pessoas que não tem conhecimento técnico) e calcular.
A diferença é que nesta versão, os valores absolutos dos valores reais das observações são somados antes de fazer a divisão para obter o erro.
Isso ajuda quando temos dados com uma quantidade significativa de zeros, pois a métrica não vai ao infinito, tornando-se inútil.
def wmape(y_true, y_pred):
return np.abs(y_true - y_pred).sum() / np.abs(y_true).sum()
Baseline Simples Do Último Valor
A solução trivial (baseline) mais simples que podemos usar é prever o valor do último período conhecido.
No nosso exemplo, isso significa usar o valor de vendas do último dia dos dados de treino para prever o valor das vendas de todos os dias dos dados de validação.
Parece simples demais para funcionar, mas já vi casos em que essa baseline superou modelos mais complexos!
from statsforecast import StatsForecast
from statsforecast.models import Naive
model = StatsForecast(models=[Naive()], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h, level=[90])
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'].values, forecast_df['Naive'].values)
print(f'WMAPE: {wmape_:.2%}')
model.plot(train, forecast_df, level=[90], unique_ids=['MEATS', 'PERSONAL CARE'], engine='matplotlib', max_insample_length=90)
Primeiro importamos duas classes, StatsForecast e Naive do módulo statsforecast.
Em seguida, criamos uma instância da classe StatsForecast e armazenamos na variável model.
Essa instância é inicializada com um argumento models que é uma lista dos modelos que queremos treinar. Por enquanto vamos usar apenas o Naive(), que é a baseline de último valor.
O argumento freq é a frequência dos dados, que no nosso caso é diária (freq="D").
O argumento n_jobs=-1 indica que queremos que o statsforecast utilize todos os núcleos disponíveis da CPU para treinar os modelos quando puder.
Igual no scikit-learn, chamamos o método fit passando o conjunto de treinamento train como argumento.
Esse método é usado para treinar os modelos que passamos no argumento models.
Com o modelo treinado, usamos o método predict com os argumentos h e level para fazer previsões.
O argumento h é o horizonte, o número de passos que queremos prever no futuro e o argumento level é uma lista com os níveis de confiança desejados, neste caso apenas 90%.
O resultado é armazenado na variável forecast_df.
| unique_id | ds | Naive | Naive-lo-90 | Naive-hi-90 | y |
|---|---|---|---|---|---|
| AUTOMOTIVE | 2014-01-01 00:00:00 | 2 | -2.67153 | 6.67153 | 0 |
| AUTOMOTIVE | 2014-01-02 00:00:00 | 2 | -4.60655 | 8.60655 | 3 |
| AUTOMOTIVE | 2014-01-03 00:00:00 | 2 | -6.09133 | 10.0913 | 0 |
| AUTOMOTIVE | 2014-01-04 00:00:00 | 2 | -7.34307 | 11.3431 | 0 |
| AUTOMOTIVE | 2014-01-05 00:00:00 | 2 | -8.44587 | 12.4459 | 1 |
Fiz o merge para adicionar a coluna y ao dataframe forecast_df para poder calcular o erro e visualizar o valor real das vendas do período de validação no gráfico.
Nesse DataFrame temos a previsão mais provável (de ponto) na coluna Naive e os limites do intervalo de confiança de 90% nas colunas Naive-lo-90 e Naive-hi-90.
Calculamos o erro com a função wmape passando como argumentos o valor real das vendas forecast_df['y'].values e a previsão forecast_df['Naive'].values.
Depois usamos a função plot para visualizar o resultado.
Os argumentos level e unique_ids especificam quais níveis de confiança e categorias queremos visualizar, para não poluir o gráfico com muitas informações.
O argumento engine usa a biblioteca plotly como padrão, que te dá um gráfico interativo. Aqui especifiquei a matplotlib porque é mais popular.
Por fim, max_insample_length é o número máximo de observações dos dados de treino que queremos visualizar no gráfico.
Se não especificarmos esse argumento, o statsforecast vai tentar plotar todos os dados de treino, o que dificulta a visualização.
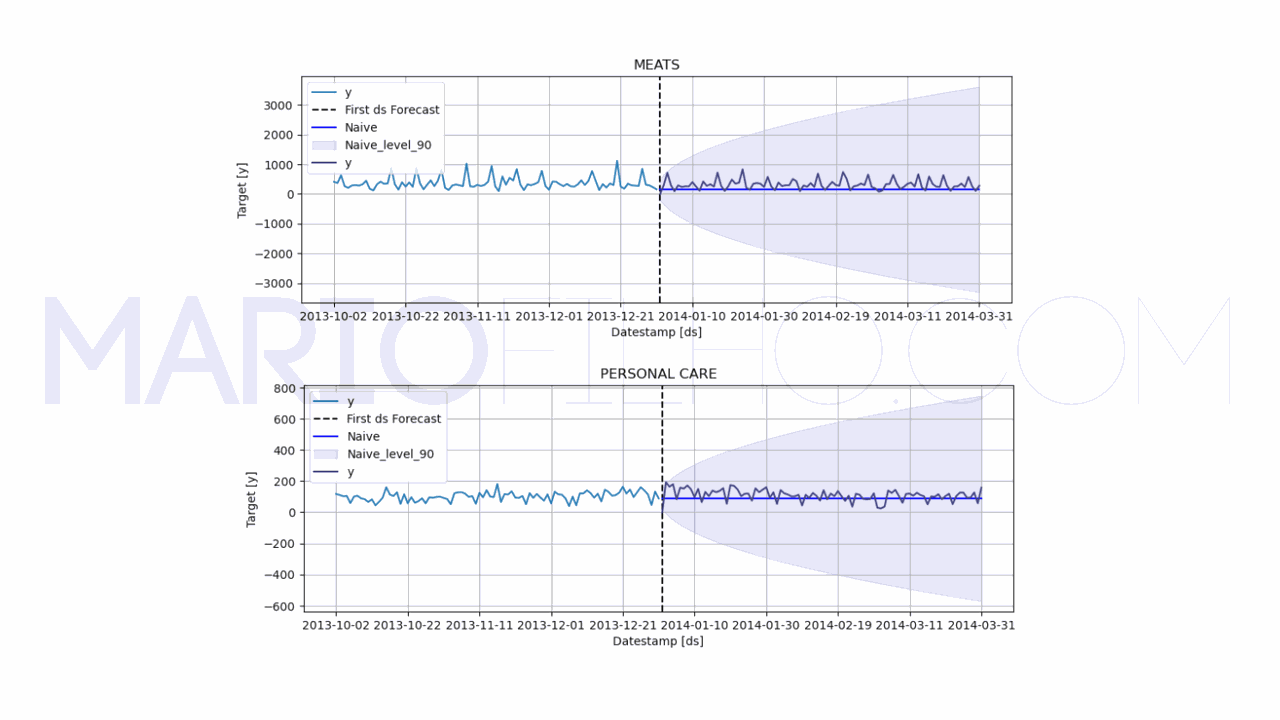
Para facilitar a visualização, coloquei apenas as categorias MEATS e PERSONAL CARE no gráfico.
No gráfico vemos:
- a linha
yem azul, que é o valor real das vendas nos últimos 90 dias de treino - a linha
yem roxo, que é o valor real das vendas nos 3 primeiros meses de validação - a linha
Naiveem azul brilhante, que é a previsão do modelo usando a baseline de último valor - a linha vertical pontilhada indicando o início dos dados de validação
- o sombreamento indicando o intervalo de confiança de 90% para as previsões
O WMAPE ficou em 0,575 ou 57,50%.
Isso é alto? Baixo? Vamos descobrir conforme treinamos os outros modelos!
Baseline Do Último Valor Com Sazonalidade
Vamos melhorar um pouco a baseline de último valor usando a sazonalidade.
Sazonalidade é um padrão que se repete no mesmo período ao longo do tempo.
Neste método, em vez de usar o último valor de um período qualquer, vamos usar o último valor de um período similar ao que queremos prever.
Por experiência, sei que o volume de vendas tende a ser diferente de acordo com o dia da semana, então vou usar o último valor do mesmo dia da semana.
Outra alternativa é usar o mesmo dia, só que do ano anterior, para capturar padrões específicos de datas comemorativas.
Nada impede de combinarmos os dois também!
Para isso vamos usar a classe SeasonalNaive do módulo statsforecast.
from statsforecast import StatsForecast
from statsforecast.models import SeasonalNaive
model = StatsForecast(models=[SeasonalNaive(season_length=7)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h, level=[90])
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'].values, forecast_df['SeasonalNaive'].values)
print(f'WMAPE: {wmape_:.2%}')
model.plot(train, forecast_df, level=[90], unique_ids=['MEATS', 'PERSONAL CARE'], engine='matplotlib', max_insample_length=90)
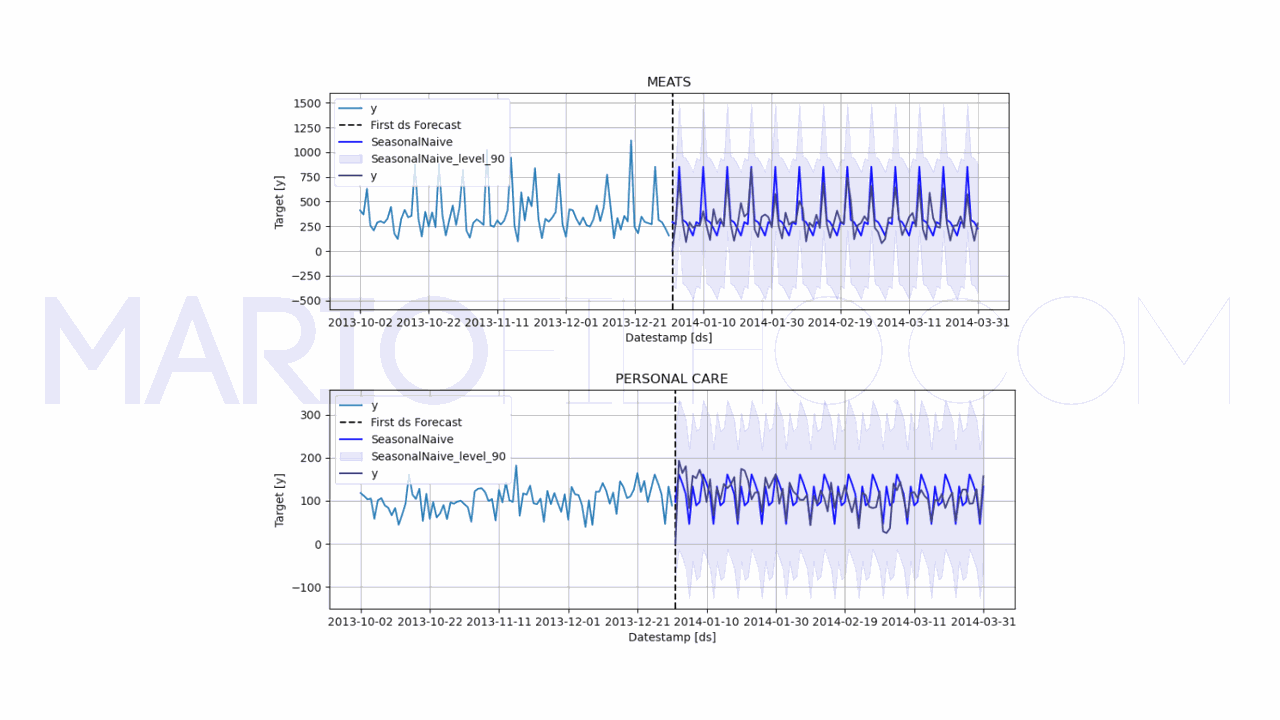
Como você vê no código acima, o único parâmetro que precisamos passar é o season_length, que é o tamanho da sazonalidade (o número de períodos até o padrão se repetir).
No nosso caso, queremos o padrão do dia da semana, então o season_length é 7.
Se tivéssemos dados de vendas por hora, por exemplo, o season_length seria 24, para capturarmos a sazonalidade pelo correr do dia.
Ao olhar o gráfico fica claro que nosso modelo está acertando mais, já que ele está considerando os picos e vales de cada dia da semana na hora da previsão em vez de ser uma linha reta.
O WMAPE caiu para 0,5091 ou 50,91%.
Vamos testar outra baseline.
Baseline de Média Móvel com Sazonalidade
Pode ser que considerando mais de um valor sazonal o WMAPE caia ainda mais.
Vamos testar a baseline de média móvel com sazonalidade.
A média móvel simples calcula a média dos valores mais recentes dentro de uma janela de períodos.
Por exemplo, se queremos usar apenas os últimos 21 dias para calcular a média, nossa janela será de 21 períodos.
Ela é uma versão suavizada da baseline de último valor.
Como queremos que ela seja sazonal, em vez de calcular a média simples dos últimos 21 dias, vamos calcular usando apenas dados do mesmo período (dia da semana).
Neste caso devemos considerar o tamanho da janela multiplicado pelo tamanho da sazonalidade.
Para calcularmos a média das últimas 4 semanas, a janela será de tamanho 4, pois vamos pegar, por exemplo, as últimas 4 segundas-feiras para prever as próximas.
Usar uma janela de tamanho 1 é o mesmo que usar a baseline de último valor com sazonalidade.
Vamos testar com uma janela de tamanho 2 para ver se conseguimos melhorar o resultado.
Na prática você deve testar diferentes janelas para ver qual se adapta melhor aos seus dados.
Para isso usamos o objeto SeasonalWindowAverage do módulo statsforecast.models.
from statsforecast import StatsForecast
from statsforecast.models import SeasonalWindowAverage
model = StatsForecast(models=[SeasonalWindowAverage(season_length=7, window_size=2)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h)
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'].values, forecast_df['SeasWA'].values)
print(f'WMAPE: {wmape_:.2%}')
model.plot(train, forecast_df, unique_ids=['MEATS', 'PERSONAL CARE'], engine='matplotlib', max_insample_length=90)
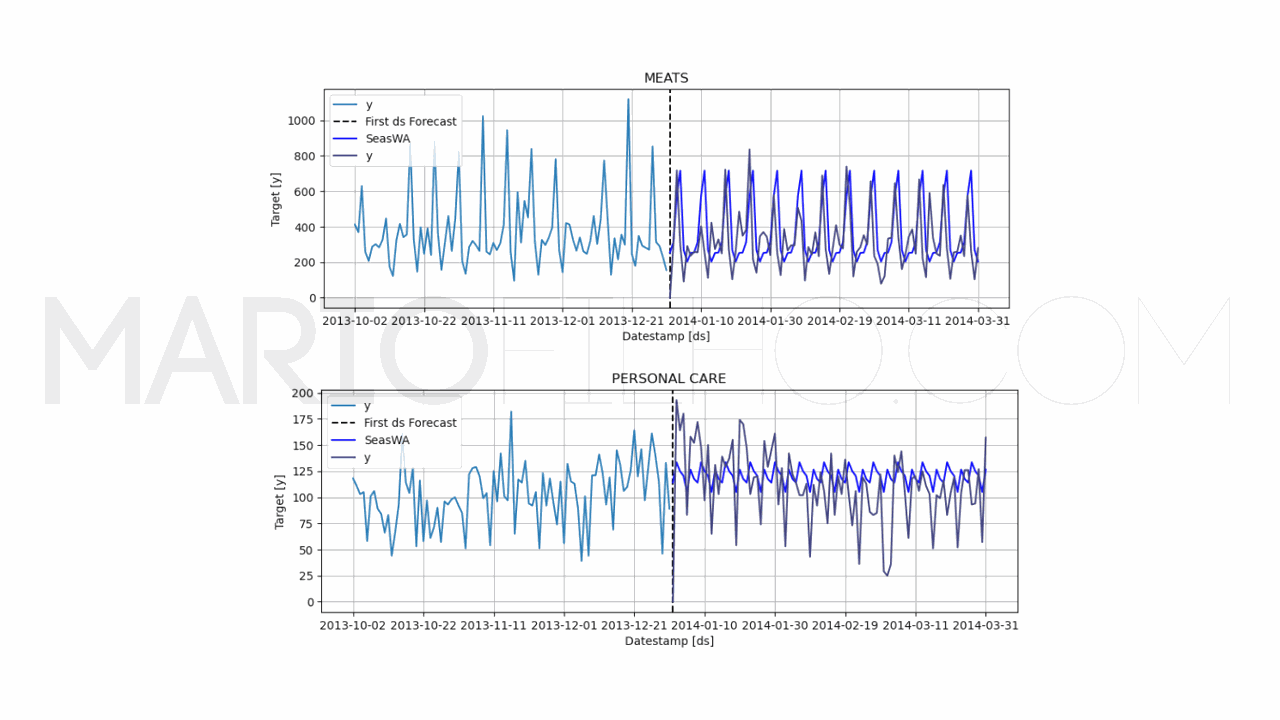
Novamente usamos o argumento season_length para definir o tamanho da sazonalidade.
Agora temos também o argumento window_size, que é o tamanho da janela (quantos períodos similares devemos considerar para calcular a média).
O pacote não dá a opção de calcular o intervalo de confiança neste caso, então temos apenas a previsão de ponto.
O WMAPE subiu para 0,5302 ou 53,02%, pior do que usando apenas a baseline de último valor com sazonalidade.
Então parece que usar apenas o último valor é melhor do que uma média de valores.
Agora que testamos 3 baselines, vamos ver como treinar modelos mais complexos para tentar reduzir o erro.
ARIMA
Um dos modelos estatísticos tradicionais mais populares é a ARIMA, que é uma abreviação de “Auto-Regressive Integrated Moving Average”.
Ela possui três componentes: o componente auto-regressivo (AR), o componente integrado (I) e o componente de média móvel (MA).
No nosso exemplo, o componente auto-regressivo (AR) olha para as vendas dos últimos dias e tenta relacioná-las com as vendas do próximo período.
Te lembra alguma baseline? Sim, a baseline de último valor.
O componente integrado (I) indica a quantidade de diferenciação que foi feita na série. Por exemplo, se a série foi diferenciada uma vez, ele será 1.
O componente de média móvel (MA) é como uma regressão linear aplicada aos erros residuais da série.
Ele não é a mesma coisa que a baseline de média móvel, que é uma média de valores.
Juntos, esses três componentes trabalham para fornecer uma previsão precisa das observações futuras.
Essa é uma explicação rápida e simplificada, mas o mais importante é entender que modelos de séries temporais geralmente vão tentar capturar aspectos como esses componentes para gerar as novas previsões.
Veja este artigo para entender mais sobre componentes de séries temporais.
Vamos usar a classe AutoARIMA do módulo statsforecast.
from statsforecast import StatsForecast
from statsforecast.models import AutoARIMA
model = StatsForecast(models=[AutoARIMA(season_length=7)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h, level=[90])
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'].values, forecast_df['AutoARIMA'].values)
print(f'WMAPE: {wmape_:.2%}')
model.plot(train, forecast_df, level=[90], unique_ids=['MEATS', 'PERSONAL CARE'], engine='matplotlib', max_insample_length=90)
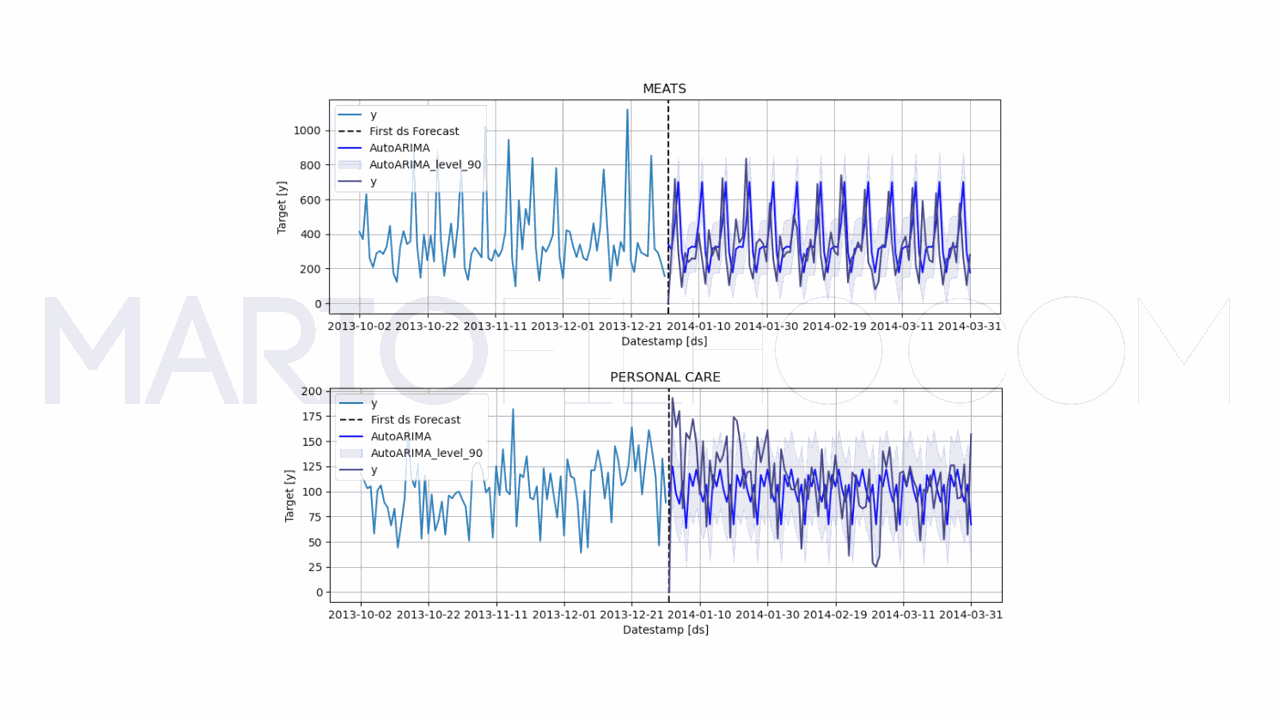
O objeto AutoARIMA vai tentar encontrar os melhores parâmetros para os três componentes do ARIMA com base no critério de informação de Akaike (AIC).
Lembra quando falei que precisamos de soluções triviais para saber se um modelo está bom ou não?
Neste caso a ARIMA resultou num erro de 55,99%, maior que nossa melhor baseline.
Então não adiantaria usar este modelo, já que usar apenas o último valor ajustado pela sazonalidade é melhor nestes dados.
Suavização Exponencial (Exponential Smoothing)
Este é um conjunto de técnicas de previsão de séries temporais que se baseia na ideia que valores mais recentes são mais importantes do que valores antigos na hora de calcular a previsão.
A Suavização Exponencial Simples (SES) é a mais simples, sendo uma média ponderada entre o valor atual e o valor acumulado da série.
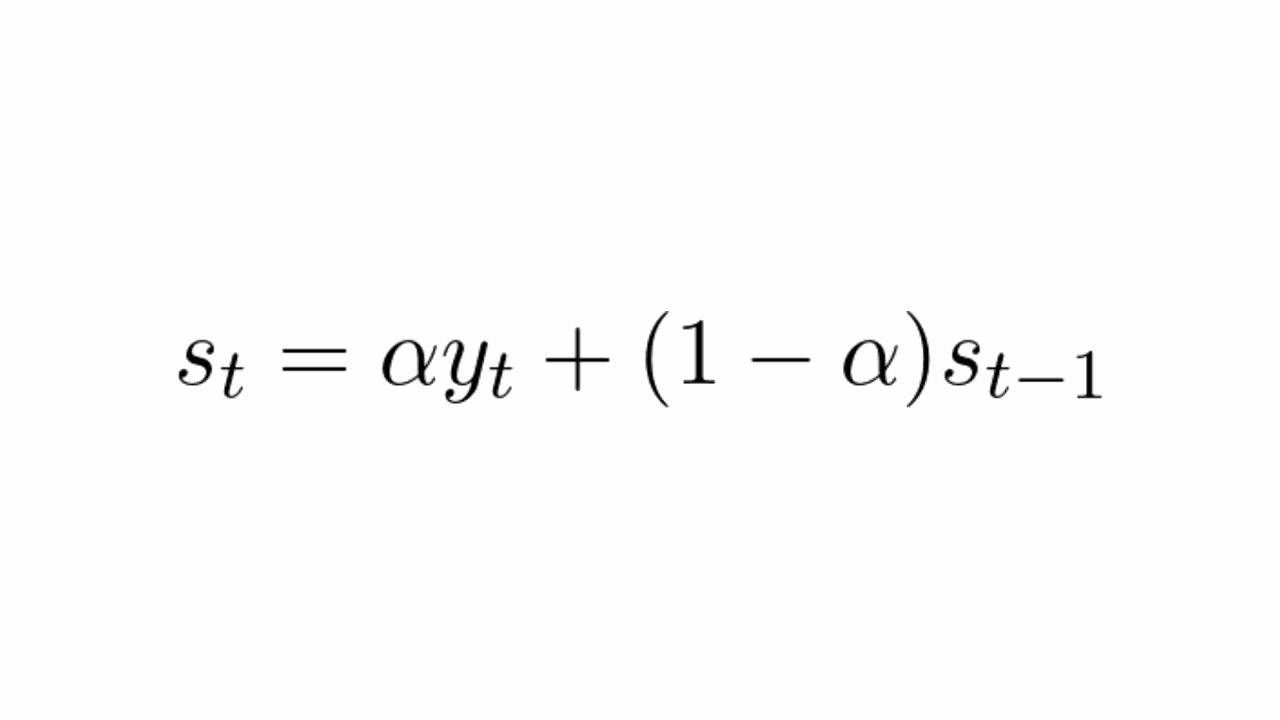
Onde:
s_té o valor da série suavizado no tempotαé o fator de suavizaçãoy_té o valor original da série no tempots_t-1é o valor da série suavizado no tempot-1
O fator de suavização é um número entre 0 e 1 que controla o quanto o valor atual da série é considerado na previsão em relação ao valor acumulado.
Ela lembra muito a média móvel, só que os pesos são determinados pelo fator de suavização.
Nós vamos usar uma técnica mais avançada de suavização, conhecida como ETS (Erro, Tendência e Sazonalidade).
Essa técnica tenta identificar os componentes da série temporal para fazer uma previsão mais precisa do que a SES.
Nossos dados possuem sazonalidade e já vimos que métodos que levam isso em conta possuem um erro menor, então vamos usar o mesmo raciocínio aqui.
Vamos usar a classe AutoETS do módulo statsforecast.
Assim como na AutoArima ele vai tentar encontrar os melhores parâmetros para os três componentes do ETS com base no critério de informação de Akaike (AIC).
from statsforecast import StatsForecast
from statsforecast.models import AutoETS
model = StatsForecast(models=[AutoETS(season_length=7)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h)
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'].values, forecast_df['AutoETS'].values)
print(f'WMAPE: {wmape_:.2%}')
model.plot(train, forecast_df, unique_ids=['MEATS', 'PERSONAL CARE'], engine='matplotlib', max_insample_length=90)
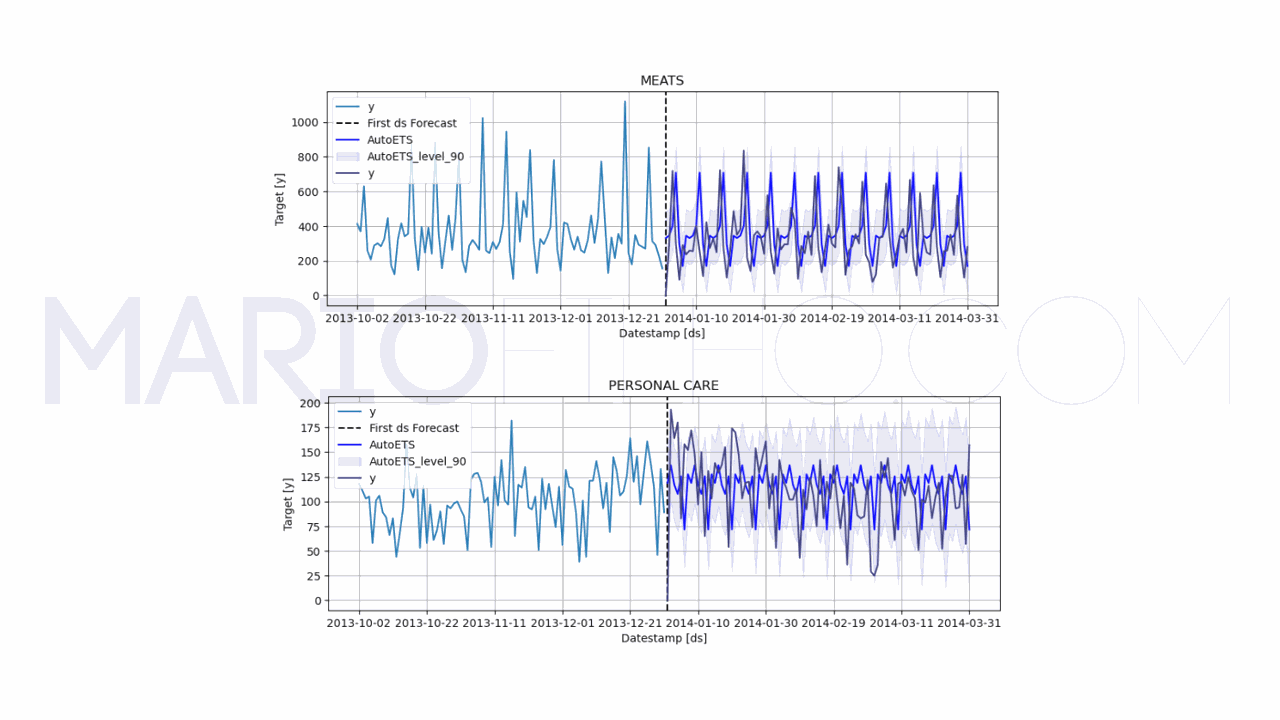
Neste objeto também temos o parâmetro season_length, que é o tamanho da sazonalidade, mas não temos o argumento levels, nos dando apenas uma previsão pontual.
O wMAPE subiu para 57,16%, sugerindo que o modelo não supera a nossa melhor baseline.
Treinando Vários Modelos de Séries Temporais Ao Mesmo Tempo
Na prática você não precisa criar um objeto StatsForecast para cada modelo que você quer treinar e repetir todo seu código. Só fiz isso aqui para deixar mais fácil de aprender.
Você pode treinar vários modelos ao mesmo tempo e comparar os resultados.
Basta passar mais modelos na lista do argumento models.
from statsforecast import StatsForecast
from statsforecast.models import Naive, SeasonalNaive, AutoARIMA
model = StatsForecast(models=[Naive(),
SeasonalNaive(season_length=7),
AutoARIMA(season_length=7)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h, level=[90])
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
Neste caso, o DataFrame forecast_df terá colunas para cada modelo que você treinou.
| unique_id | ds | Naive | Naive-lo-90 | Naive-hi-90 | SeasonalNaive | SeasonalNaive-lo-90 | SeasonalNaive-hi-90 | AutoARIMA | AutoARIMA-lo-90 | AutoARIMA-hi-90 | y |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AUTOMOTIVE | 2014-01-01 00:00:00 | 2 | -2.67153 | 6.67153 | 1 | -15.373 | 17.373 | 1.48352 | -2.24143 | 5.20848 | 0 |
| AUTOMOTIVE | 2014-01-02 00:00:00 | 2 | -4.60655 | 8.60655 | 2 | -14.373 | 18.373 | 1.07535 | -2.6496 | 4.8003 | 3 |
| AUTOMOTIVE | 2014-01-03 00:00:00 | 2 | -6.09133 | 10.0913 | 6 | -10.373 | 22.373 | 2.09102 | -1.63393 | 5.81597 | 0 |
| AUTOMOTIVE | 2014-01-04 00:00:00 | 2 | -7.34307 | 11.3431 | 4 | -12.373 | 20.373 | 3.28571 | -0.439237 | 7.01067 | 0 |
| AUTOMOTIVE | 2014-01-05 00:00:00 | 2 | -8.44587 | 12.4459 | 0 | -16.373 | 16.373 | 1.8917 | -1.83325 | 5.61665 | 1 |
