Quando tratamos da previsão de séries temporais um modelo amplamente utilizado é a regressão linear. Apesar de simples, ele tem se mostrado bastante útil em aplicações reais.

Uma forma muito simples de criar um modelo para este caso é usar os dados anteriores da própria variável de interesse para prever o atual. É possível criar modelos que buscam prever estas séries utilizando outros atributos, o que em alguns casos vai melhorar a precisão dos mesmos.

Neste artigo quero demonstrar a maneira mais simples, usando uma regressão linear nos dados históricos da própria variável de interesse. O código disponibilizado está num formato adequado para que o leitor entenda o que está acontecendo, por isso ele pode ter partes que poderiam ser otimizadas num ambiente de produção, mas foi uma escolha, de acordo com o objetivo educacional do artigo, deixa-las assim.

O código completo, e os dados, estão disponíveis aqui.

Veja também este artigo atualizado sobre previsão de séries temporais com scikit-learn

Índice

Descrição dos dados

Os dados utilizados correspondem à “prime rate” no Brasil. A “prime rate” é a taxa de juros bancários para clientes preferenciais, ou seja, aplicada a clientes com baixo risco de inadimplência em operações de alto valor. Vamos usar os valores desta taxa nos últimos 6 meses para prever o próximo.

Prime Rate

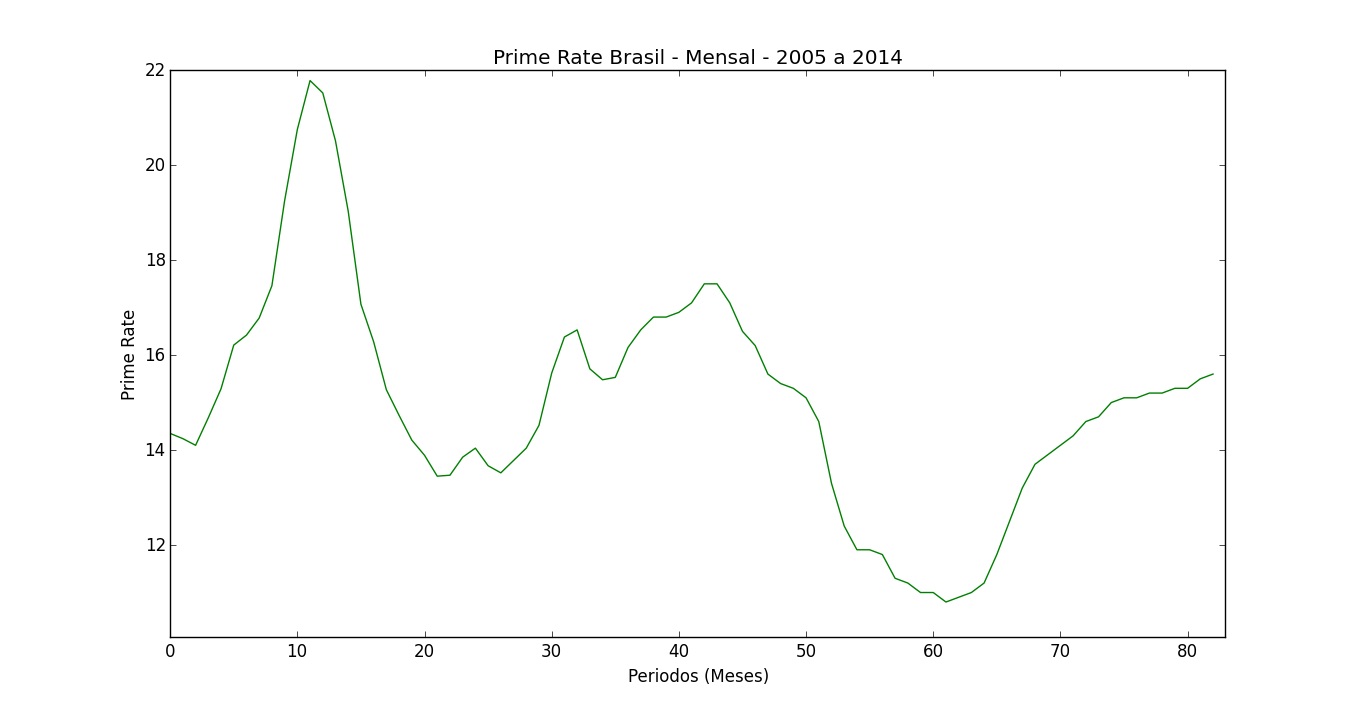
Temos dados mensais de janeiro de 2005 até novembro de 2014. Eles são originalmente divulgados pelo Banco Central do Brasil, mas foram obtidos na plataforma Quandl.

Observação importante: não use as informações deste artigo como base para tomar quaisquer decisões, inclusive financeiras, ou de investimentos. Este é um artigo educacional e serve apenas para demonstrar o uso de uma ferramenta de machine learning para a previsão de séries temporais.

Modelos utilizados para comparação

Para comparar o desempenho da regressão linear neste problema, vou utilizar outros dois métodos válidos para previsão de séries temporais:

Valor do último mês: a previsão para o próximo mês é simplesmente o mesmo valor da variável no último mês.

Média Móvel: a previsão para o próximo mês é a média dos valores dos últimos 6 meses.

Métrica de avaliação

Vamos utilizar o Erro Percentual Absoluto Médio (em inglês, MAPE). É uma métrica bastante utilizada na área de previsões de séries temporais, e se refere à média do percentual de erros cometidos nas previsões, desconsiderando a direção (acima ou abaixo do real).

Além deste erro, também avaliaremos o Erro Médio Absoluto (MAE, em inglês), que é a média dos erros absolutos (ignorando o sinal positivo ou negativo). Assim sabemos melhor quanto estamos desviando dos valores reais nas unidades originais.

Do ponto de vista prático, para que possamos justificar o uso da regressão linear em vez dos métodos mais simples, ela deve apresentar um erro médio menor do que o erro das outras opções.

Para quem quiser ser um pouco mais rigoroso, vou usar um teste estatístico pareado (Wilcoxon Signed-Rank) para avaliar as duas alternativas que oferecerem os menores erros. Levando em consideração algumas suposições sobre os dados, ele basicamente nos diz a probabilidade da diferença entre os erros dos dois métodos ser puramente por sorte, e não por alguma característica especial que torne um modelo melhor do que o outro.

Na prática, na maioria das vezes a decisão de usar um modelo ou outro é feita diante da comparação entre a melhora no desempenho e o esforço necessário para coloca-lo em funcionamento. Alguns modelos que passam pelo teste estatístico, mas são muito complicados, nunca serão implementados, enquanto outros, mais simples, que não passam pelo rigor do teste, serão utilizados.

Módulos Python utilizados

Para rodar o script deste artigo são necessários os seguintes módulos Python: Numpy, Pandas e Scikit-learn. Caso queira efetuar o teste pareado também é necessário ter Scipy. Para reproduzir o gráfico, é necessário Matplotlib.

Definindo as funções das métricas de avaliação

Para o MAE vamos utilizar a implementação disponível no scikit-learn. Como ele não possui uma função para computar o MAPE, nós precisamos cria-la.

#Define função para calcular o MAPE
def mape(y_pred,y_true):
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100

Carregando e formatando os dados

Os dados estão num CSV em formato de tabela. Após carregarmos o CSV na memória usando Pandas precisamos organizar os dados para fazer a previsão. O scikit-learn não se dá muito bem com Pandas, então além de preparar os dados no formato correto para alimentar o modelo, vamos coloca-los em arrays do numpy.

data = pd.read_csv('prime.csv',header=0,index_col=0).sort_index()
x_data = []
y_data = []

# Formata de maneira que cada linha da matriz X seja composta pelos 6 meses anteriores.

for d in xrange(6,data.shape[0]):
    x = data.iloc[d-6:d].values.ravel()
    y = data.iloc[d].values[0]
    x_data.append(x)
    y_data.append(y)

A matriz de atributos terá 6 colunas, uma para cada mês anterior ao que queremos prever, e o vetor com a variável dependente terá o valor a ser previsto (próximo mês). Para isso vamos começar pelo sétimo mês disponível, que é o número seis no loop porque, em Python, o primeiro elemento é indexado como zero.

Treinando o modelo e fazendo as previsões

Dados financeiros normalmente mudam de regime com frequência, então vamos treinar um novo modelo a cada mês. O primeiro mês a ser previsto será o 31º disponível após a transformação dos dados. Assim temos pelo menos 30 exemplos para treinar o primeiro modelo. Em tese quanto mais dados para treinar, melhor.

Esta maneiras de treinar e validar o modelo é chamada de método de janela expansiva.

Para cada mês vamos armazenar o valor previsto pelos três métodos e o valor verdadeiro.

#Itera pela série temporal treinando um novo modelo a cada mês
end = y_data.shape[0]
for i in range(30,end):

    x_train = x_data[:i,:]
    y_train = y_data[:i]

    x_test = x_data[i,:]
    y_test = y_data[i]


    model = LinearRegression(normalize=True)
    model.fit(x_train,y_train)

    y_pred.append(model.predict(x_test).reshape(1,-1))[0]
    y_pred_last.append(x_test[-1])
    y_pred_ma.append(x_test.mean())
    y_true.append(y_test)

Avaliação dos resultados

Após a conclusão das previsões, transformamos as listas em arrays do numpy novamente e computamos as métricas.

print '\nMean Absolute Percentage Error'
print 'MAPE Regressão Linear', mape(y_pred,y_true)
print 'MAPE Último Valor', mape(y_pred_last,y_true)
print 'MAPE Média Móvel', mape(y_pred_ma,y_true)


print '\nMean Absolute Error'
print 'MAE Regressão Linear', mean_absolute_error(y_pred,y_true)
print 'MAE Último Valor', mean_absolute_error(y_pred_last,y_true)
print 'MAE Média Móvel', mean_absolute_error(y_pred_ma,y_true)

Mean Absolute Percentage Error
MAPE Regressão Linear 1.87042556874
MAPE Último Valor 2.76774390378
MAPE Média Móvel 7.90386089172

Mean Absolute Error
MAE Regressão Linear 0.284087187881
MAE Último Valor 0.427831325301
MAE Média Móvel 1.19851405622

Vemos que o melhor modelo é a regressão linear, seguido por usar o valor do último mês, e um resultado bastante ruim com o método da média móvel.

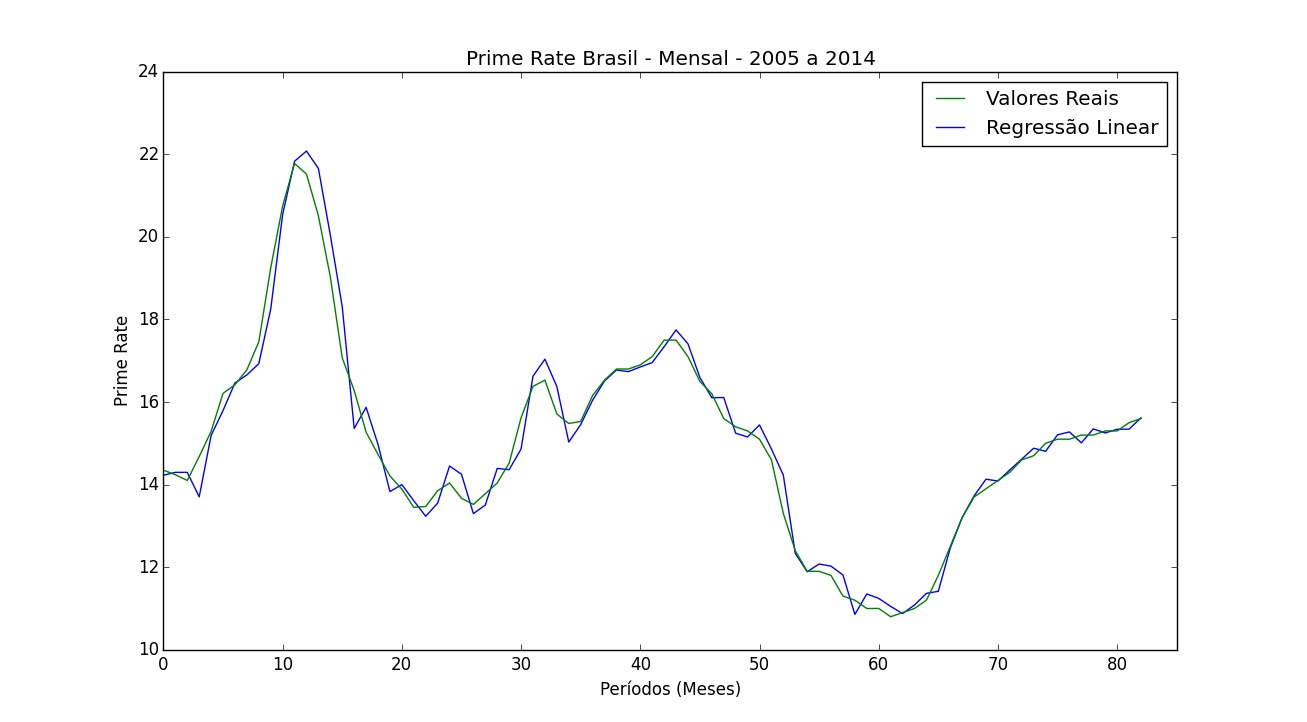
Prime Rate Linear Regression

Teste Wilcoxon Signed-Rank - Opcional

Vamos usar um teste pareado nos erros absolutos da regressão linear e do método que utiliza o valor do último mês para ver se a diferença entre eles é significativa do ponto de vista estatístico. Ou seja, qual é a probabilidade da diferença entre o erro dos dois modelos ser apenas por sorte.

error_linreg = abs(y_true - y_pred)
error_last = abs(y_true - y_pred_last)
print '\nWilcoxon P-value', wilcoxon(error_linreg,error_last)[1]/2.

Wilcoxon P-value 0.000353384009751

O p-value reportado por esta função é relativo a um teste de duas caudas, ou seja, testa se as médias são diferentes. No nosso caso, estamos mais interessados em saber se uma média é menor do que a outra, ou seja, um teste de uma cauda. A forma mais fácil de converter este número para o que nós desejamos é dividi-lo por 2.

O p-value mínimo mais aceito pela comunidade científica para determinar que há uma diferença entre as médias é de 0,05. Neste caso estamos bem abaixo, nosso p-value é menor do que 0,001, então conseguimos determinar que a probabilidade da diferença de performance entre os modelos ser apenas por sorte é mínima. Podemos rejeitar a hipótese que eles oferecem o mesmo desempenho, e favorecer o uso da regressão linear.

Vale a pena ressaltar que, ao usar estes testes, é importante continuar a coletar dados mesmo após atingir significado estatístico, para confirmar o resultado. Parar de coletar assim que se atinge o nível desejado do p-value pode levar a resultados falsos.

Sugestões para melhorar o modelo

Nós criamos o modelo mais simples possível, baseado apenas nos valores históricos da série. Abaixo deixo algumas sugestões que podem ser implementadas para possivelmente reduzir o erro.

Boosting

Boosting é uma técnica que treina vários modelos nos mesmos dados, a diferença é que cada modelo é treinado nos erros residuais dos anteriores. Apesar de haver o risco de overfitting caso não seja feita uma boa validação, esta é uma técnica que apresenta bastante sucesso na prática.

Criação de mais atributos

Utilizamos apenas os valores dos últimos seis meses como variáveis independentes. Se adicionarmos mais variáveis que sejam correlacionadas com a variável dependente, podemos melhorar o modelo. Além disso, podemos adicionar atributos baseados em transformações, como elevar os valores ao quadrado, para capturar relações não lineares.

Usar outros modelos

Regressão linear não é a única opção nestes casos. Existem modelos baseados em alterações da regressão linear, redes neurais (LSTM), SVMs, e decision trees que podem apresentar um desempenho melhor.

Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.