Índice
- O Que é Mean Average Precision?
- Qual a Fórmula da Mean Average Precision?
- Como Interpretar a Mean Average Precision?
- Como Calcular a Mean Average Precision em Python?
- Qual a Diferença Entre Mean Average Precision e NDCG?
- Qual a Diferença Entre Mean Average Precision e Mean Reciprocal Rank?
O Que é Mean Average Precision?
Mean Average Precision (MAP) é uma métrica de avaliação em machine learning comumente usada para medir a performance de sistemas de recomendação e busca.
Um outro caso de uso interessante é na avaliação de modelos de segmentação de imagem, onde você precisa detectar e segmentar vários objetos em uma mesma imagem.
Uma analogia mais divertida para lembrar o que é a MAP é a seguinte:
Imagine que você está organizando um jogo de caça ao tesouro.

Você escondeu vários tesouros em diferentes locais e os jogadores têm que encontrá-los.
O objetivo é encontrar o maior número de tesouros possível, mas também é importante encontrá-los rapidamente.
A MAP é como a pontuação final do jogo, levando em conta tanto a quantidade de tesouros encontrados quanto o tempo gasto para encontrá-los.
Ela leva em conta a ordem dos itens recomendados e não apenas a quantidade de itens relevantes retornados.
Um sistema de recomendação que coloca itens relevantes no início dos resultados terá um MAP maior do que outro que os coloca no final.
Qual a Fórmula da Mean Average Precision?
A fórmula da MAP é a média aritmética das Average Precisions (AP) de cada lista de resultados retornada pelo modelo.
Nestes exemplos vou tratar cada lista como recomendações para um usuário.
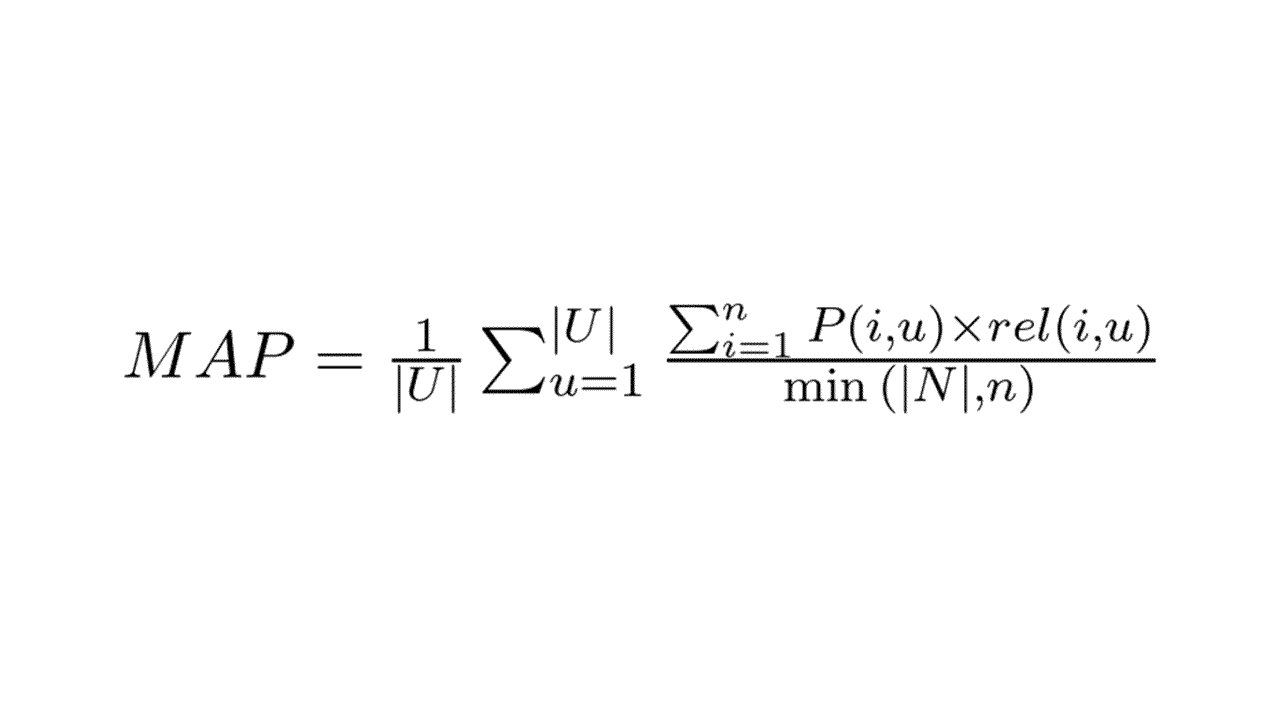
Onde:
- |U| é o número total de usuários
- u é o usuário atual
- |N| é o número total de itens relevantes para o usuário u
- n é o número de itens recomendados para o usuário u
- P(i, u) é a precisão para a posição i e usuário u
- rel(i, u) é a relevância do item na posição i para o usuário u (1 para relevante e 0 para irrelevante)
- min(|N|, n) retorna o menor valor entre o total de itens relevantes que poderíamos recomendar e o tamanho da lista de recomendações
Preste atenção que a MAP só considera a precisão de posições com itens relevantes.
A precisão de posições com itens irrelevantes é zerada.
Como você pode ver, a fórmula da MAP envolve duas médias: a média aritmética das Average Precisions e a média das listas de resultados.
Em português seria algo como: “a média aritmética das precisões médias”.
No caso, a “mean” significa a média externa, calculada sobre as APs de cada lista de resultados.
E a “average” significa a média interna, calculada sobre cada lista de resultados.
Vamos entender melhor com um exemplo na próxima seção.
Como Interpretar a Mean Average Precision?
Primeiro precisamos calcular a Average Precision (AP).
A Average Precision (AP) é calculada sequencialmente sobre cada lista de itens recomendados pelo modelo.
Vamos entender melhor com um exemplo:
| Posição | Item Recomendado | Relevante? - rel(i,u) | Precisão - P(i,u) |
|---|---|---|---|
| 1 | A | 1 | 1 |
| 2 | B | 0 | 0 |
| 3 | C | 1 | 0,67 |
| 4 | D | 0 | 0 |
| 5 | E | 0 | 0 |
O exemplo acima mostra como calcular a Average Precision usando uma tabela com cinco itens recomendados pelo sistema e sua relevância para o usuário.
Os itens podem ser produtos de supermercado, filmes, músicas, vídeos, resultados de busca, etc.
A relevância poderia ser um número qualquer (como uma nota de uma a cinco estrelas), mas você precisa definir um limiar para determinar se um item é relevante ou não.
A Average Precision precisa de relevâncias binárias, ou seja, 1 se o item é relevante e 0 se não é relevante.
Na primeira posição, o item recomendado é A e ele é relevante, então a precisão é 1/1 * 1 (um item relevante de um recomendado multiplicado pela relevância do item desta posição).
Na segunda posição, o item recomendado é B e não é relevante, então apesar da precisão ser 1/2 (um item relevante de dois recomendados), ela é zerada porque o item da posição 2 não é relevante.
Na terceira posição, o item recomendado é relevante, então a precisão é calculada como 2/3 * 1 = 0,67 (dois itens relevantes de três recomendados).
Nas quarta e quinta posições, os itens recomendados D e E não são relevantes, então a precisão fica zerada.
Para calcular a AP, você soma a precisão de cada posição e divide pelo mínimo entre a quantidade de itens relevantes que poderiam ser recomendados e o tamanho da lista.
Neste caso, se apenas os itens A e C forem relevantes para este usuário considerando todo o catálogo de itens, a AP é 1,67 / 2 = 0,835.
Se o catálogo tiver 3 itens relevantes (A, B e F), mas um deles não foi recomendado, a AP seria 1,67 / 3 = 0,557.
Agora suponha que o catálogo de itens tenha 6 itens relevantes para este usuário.
Como a lista pode ter apenas 5 itens, a AP ficaria em 1,67 / 5 = 0,334.
Isso faz com que a MAP sempre retorne um valor entre 0 e 1.
Sendo 0 o pior valor possível e 1 o melhor valor possível.
No fim, você calcula a média das APs de cada lista de resultados do seu conjunto total de usuários.
Como Calcular a Mean Average Precision em Python?
Apesar do scikit-learn ter uma função para calcular a MAP, ela não é muito intuitiva.
As funções do scikit-learn devem seguir um padrão, o que acaba tornando algumas delas mais complicadas do que deveriam ser.
Por isso, vamos implementar a MAP em Python puro.
recomendacoes = [[1,2,3,4,5],
[3,4,2,1,5],
[5,4,3,2,1]]
itens_relevantes = [[1,3,7,8,9,10],
[4,5],
[3,1,7,9]]
lista_precisoes = list()
for u, lista in enumerate(recomendacoes):
ap = 0
contagem_relevantes = 0
contagem_total = 0
for i in range(len(lista)):
contagem_total += 1
if lista[i] in itens_relevantes[u]:
contagem_relevantes += 1
ap += contagem_relevantes / contagem_total
ap = ap / min(len(itens_relevantes[u]), len(lista))
lista_precisoes.append(ap)
map = sum(lista_precisoes) / len(lista_precisoes)
Na prática você terá várias listas de itens recomendados e relevantes que podem ser, por exemplo, de usuários diferentes.
Vamos simular esse cenário usando as variáveis recomendacoes e itens_relevantes.
Cada linha representa um usuário diferente, então temos um total de três usuários.
O conjunto de itens relevantes é diferente para cada usuário.
Num sistema de recomendação de filmes, por exemplo, alguns usuários preferem filmes de ação, outros preferem comédias, outros preferem filmes de terror e assim vai.
A variável lista_precisoes é uma lista vazia que vai armazenar a AP de cada usuário.
Vamos processar uma lista por vez no loop for u, lista in enumerate(recomendacoes):.
Dentro desse loop principal, temos outro loop for i in range(len(lista)):, que vai percorrer cada lista, verificando se cada item recomendado está na lista de relevantes.
Para cada item recomendado verificado, adicionamos 1 à variável contagem_total.
Esse é apenas um contador para sabermos em qual posição estamos.
Caso o item recomendado esteja na lista de relevantes, adicionamos 1 à variável contagem_relevantes.
Esta é a contagem de quantos itens relevantes foram recomendados até o momento.
Além disso, calculamos a precisão para aquela posição, que é a proporção de itens relevantes encontrados até a posição atual, e adicionamos à variável ap.
Note que quando o item é irrelevante nós não somamos nada à variável ap.
Após verificarmos toda a lista do usuário atual, calculamos a Average Precision dividindo a variável ap pelo mínimo entre número de itens relevantes possíveis e o tamanho da lista de recomendações min(len(itens_relevantes[u]), len(lista)).
Adicionamos esse valor à lista lista_precisoes para, no fim, calcular a média das APs de todos os usuários e finalmente obter a MAP.
Qual a Diferença Entre Mean Average Precision e NDCG?
Expliquei a diferença entre Mean Average Precision e NDCG neste post.
Qual a Diferença Entre Mean Average Precision e Mean Reciprocal Rank?
Expliquei a diferença entre Mean Average Precision e Mean Reciprocal Rank neste post.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.