Índice
- O Que São Séries Temporais?
- Quais São Os Principais Tipos De Séries Temporais?
- Quais São Os Componentes De Uma Série Temporal?
- O Que É Lag Na Análise de Séries Temporais?
- O Que é Autocorrelação Numa Série Temporal?
- Como Machine Learning É Usado Com Séries Temporais?
O Que São Séries Temporais?
Séries temporais são conjuntos de dados que são observados ao longo do tempo.
Elas são amplamente utilizadas em campos como meteorologia, economia e finanças.
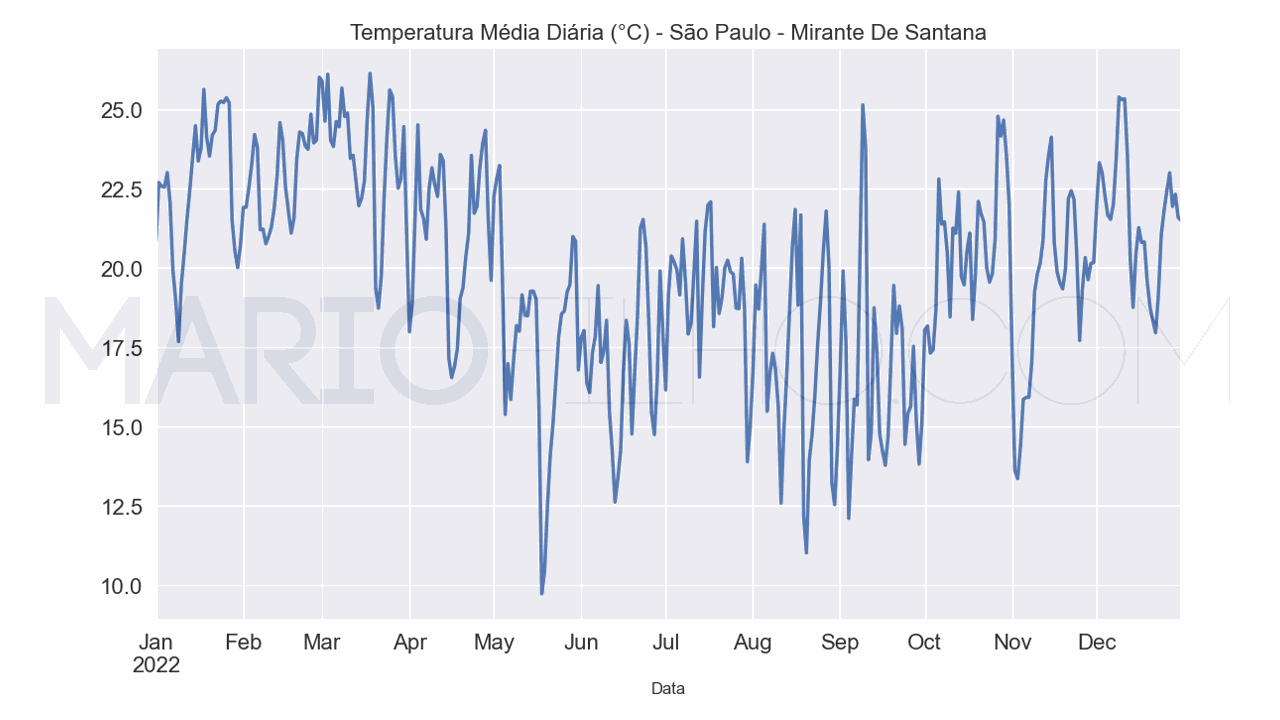
Cada amostra é marcada com um instante de tempo específico.
No exemplo acima temos uma série temporal da média da temperatura diária, em Celsius, medida no Mirante de Santana na cidade de São Paulo.
Cada dia é uma amostra com sua própria temperatura e data.
Essas amostras estão ordenadas no tempo, e é por isso que chamamos isso de série temporal.
O período de tempo entre cada amostra é chamado de intervalo de amostragem (no exemplo acima, o intervalo é diário).
Ele pode variar desde nanossegundos até anos!
Um exemplo de série temporal em nanossegundos é a sequência de negociações de uma ação na bolsa de valores.
Cada nova negociação é uma amostra com seu próprio momento no tempo.
Você vai encontrar o termo “timestamp” que é o nome dado ao instante específico de tempo em que uma amostra é observada.
| Timestamp | Negociações |
|---|---|
| 2023-01-01 00:00:00.00000000 | 10 |
| 2023-01-01 00:00:00.000000001 | 2 |
| 2023-01-01 00:00:00.000000230 | 7 |
| 2023-01-01 00:00:00.000000720 | 2 |
| 2023-01-01 00:00:01.000000004 | 1 |
Um exemplo de série temporal em anos é a temperatura média da Terra.
Neste caso, as diferenças demoram anos para se manifestar, então não vale a pena registrar estes dados em intervalos de tempo menores.
| Timestamp | Temperatura (Cº) |
|---|---|
| 2023-12-31 00:00:00 | 15.1 |
| 2024-12-31 00:00:00 | 15.1 |
| 2025-12-31 00:00:00 | 15.2 |
| 2026-12-31 00:00:00 | 15.2 |
| 2027-12-31 00:00:00 | 15.3 |
Como você viu na primeira tabela, os dados não precisam ser coletados em intervalos de tempo regulares.
Quais São Os Principais Tipos De Séries Temporais?
Existem algumas características de séries temporais que podem nos ajudar a decidir a direção de nossa análise.
Algumas delas são: número de variáveis, estacionariedade e regularidade.
Diferença Entre Série Temporal Univariada e Multivariada
A primeira característica que você deve levar em conta é se a série temporal possui apenas uma ou mais variáveis.
Chamamos de série temporal univariada aquela que possui apenas uma variável, um dado observado em cada timestamp.
Um exemplo de série temporal univariada é a sequência diária de temperaturas de uma cidade.
| Data | TEMPERATURA DO AR - BULBO SECO, HORARIA (°C) |
|---|---|
| 2022-12-27 00:00:00 | 23.0042 |
| 2022-12-28 00:00:00 | 21.9417 |
| 2022-12-29 00:00:00 | 22.325 |
| 2022-12-30 00:00:00 | 21.5958 |
| 2022-12-31 00:00:00 | 21.5083 |
Por outro lado, uma série temporal multivariada pode ter mais de um dado registrado para cada timestamp.
Imagine que agora, além da temperatura, nós começamos a medir umidade, pressão atmosférica e velocidade do vento diariamente para a mesma cidade.
| Data | TEMPERATURA DO AR - BULBO SECO, HORARIA (°C) | PRESSAO ATMOSFERICA AO NIVEL DA ESTACAO, HORARIA (mB) | VENTO, VELOCIDADE HORARIA (m/s) | UMIDADE RELATIVA DO AR, HORARIA (%) |
|---|---|---|---|---|
| 2022-12-27 00:00:00 | 23.0042 | 924.333 | 1.325 | 71.5 |
| 2022-12-28 00:00:00 | 21.9417 | 923.321 | 2.30833 | 76.25 |
| 2022-12-29 00:00:00 | 22.325 | 924.617 | 2.50833 | 73.6667 |
| 2022-12-30 00:00:00 | 21.5958 | 926.587 | 1.57917 | 80.1667 |
| 2022-12-31 00:00:00 | 21.5083 | 926.725 | 1.44583 | 77.9583 |
Neste caso teremos 4 variáveis para cada registro no tempo.
Em geral, séries multivariadas vão permitir que você faça análises e previsões mais precisas, já que dificilmente existe um fenômeno que não seja influenciado por outros fatores além de si mesmo.
Diferença Entre Série Temporal Estacionária e Não Estacionária
A segunda característica importante é se a série temporal é estacionária ou não.
Uma série temporal estacionária é aquela em que características estatísticas, como a média e a variância, não mudam significativamente com o passar do tempo.
Por exemplo, no caso da média, não importa o conjunto de observações que você escolher, a média aproximada será sempre a mesma.
É raro encontrar exemplos de séries temporais estacionárias reais então geralmente usamos exemplos simples como a sequência de cara ou coroa de uma moeda.
Se você jogar a mesma moeda 100 vezes por dia e anotar o resultado, seja qual for o período de tempo que você escolher, a média de caras e coroas será próxima de 50%.
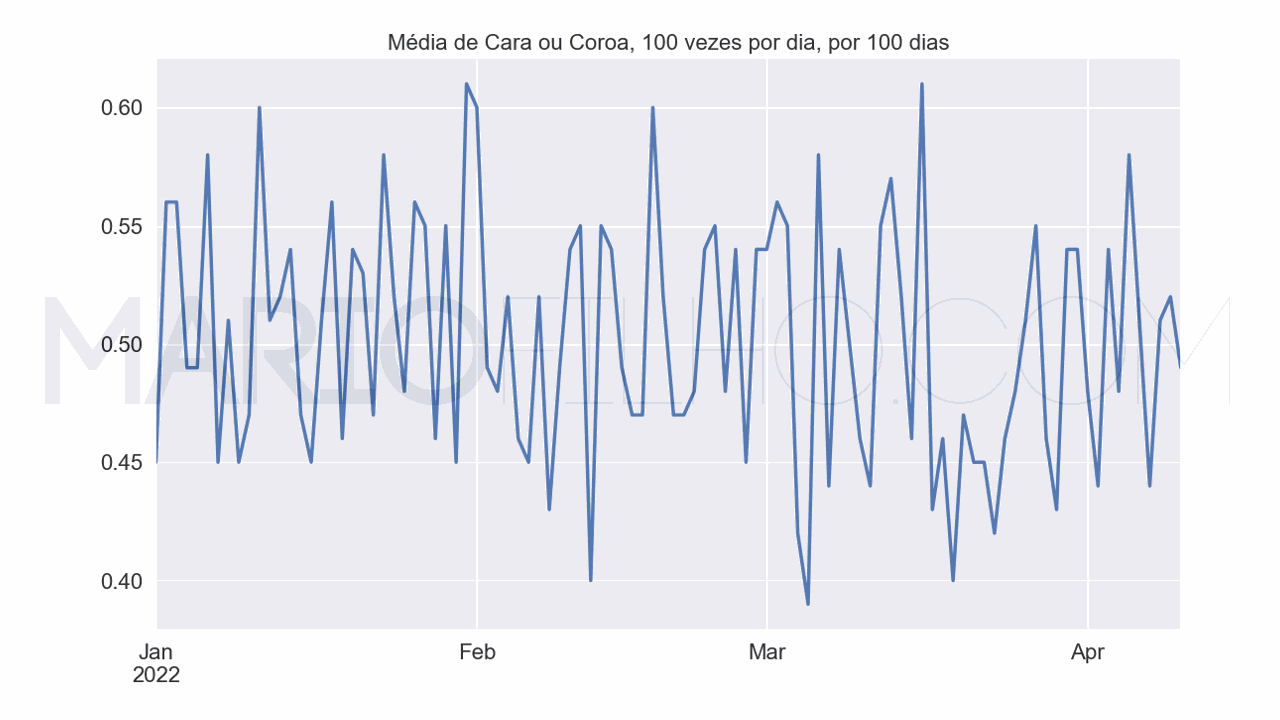
Por outro lado, numa série temporal não estacionária as características estatísticas mudam ao longo do tempo.
Como falei, na prática a maioria das séries temporais não são estacionárias e você deve levar isso em conta ao fazer suas análises.
Caso você vá fazer gráficos para entender melhor a série, isso geralmente não é um problema, mas quando você for fazer modelagem, é importante “estacionarizar” a série temporal.
Uma técnica muito utilizada para fazer isso é a diferenciação: simplesmente a subtraia os valores de uma observação pelo valor da observação anterior.
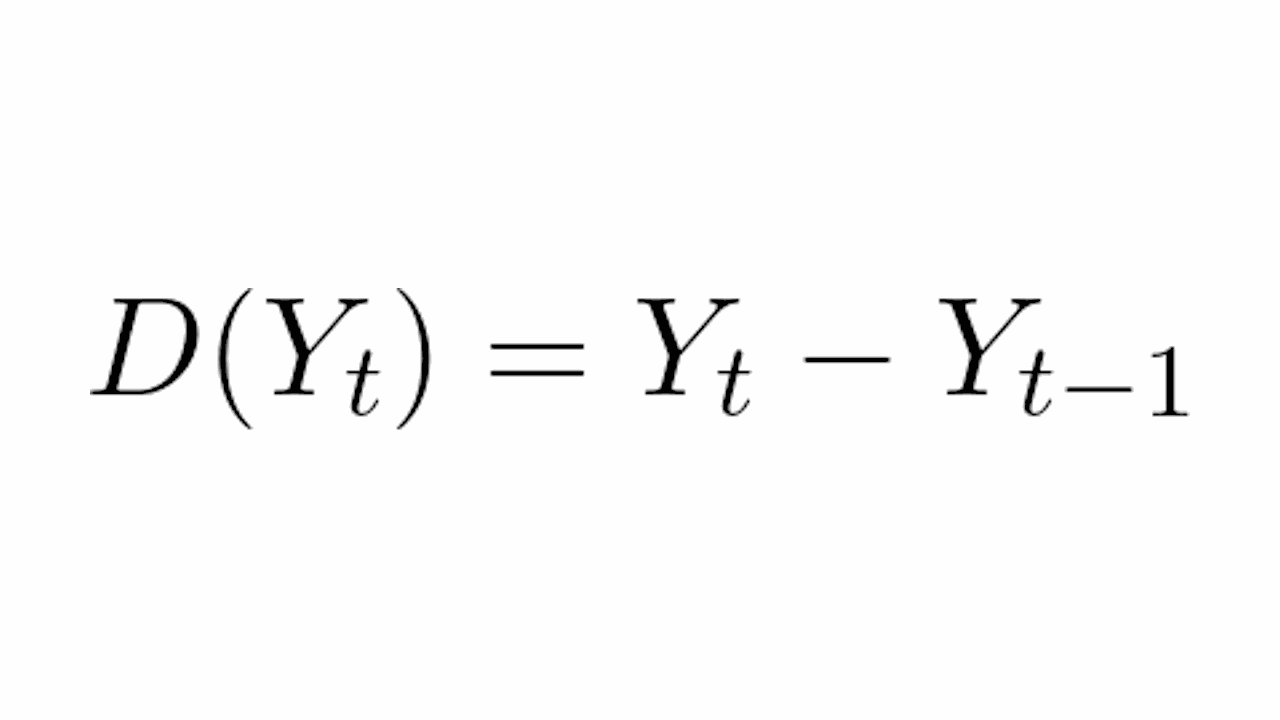
Onde:
Y_té o valor da série original no momentotY_t-1é o valor da série original no momentot-1D(Y_t)é o valor da série diferenciada no momentot
Veja como a média da temperatura diária em São Paulo fica mais estável após a diferenciação.
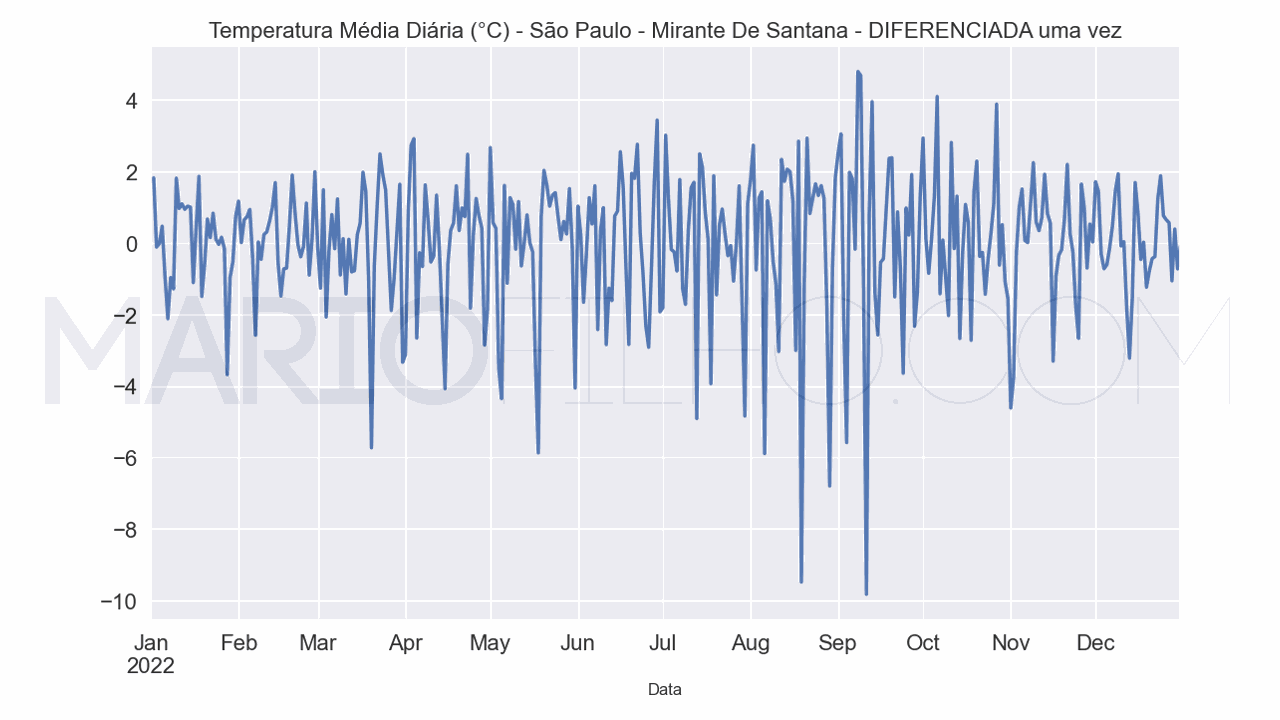
Você pode diferenciar a série temporal quantas vezes quiser, mas geralmente uma vez é suficiente.
Depois de verificar que ela está aproximadamente estacionária, você pode começar a modelagem.
Diferença Entre Série Temporal Regular e Irregular
A diferença principal entre uma série temporal regular e irregular é a forma como esses dados são coletados.
Como o próprio nome sugere, uma série temporal regular é coletada de forma consistente e regular.
Por exemplo, se você estiver medindo a temperatura de hora em hora, você terá registros com intervalos iguais de tempo.
| Data | TEMPERATURA DO AR - BULBO SECO, HORARIA (°C) |
|---|---|
| 2022-12-27 00:00:00 | 23.0042 |
| 2022-12-28 00:00:00 | 21.9417 |
| 2022-12-29 00:00:00 | 22.325 |
| 2022-12-30 00:00:00 | 21.5958 |
| 2022-12-31 00:00:00 | 21.5083 |
Já uma série temporal irregular pode ter intervalos de tempo diferentes entre registros.
No exemplo abaixo, temos dados simulados de um sensor que gera registros de alerta cada vez que a maré passa de um determinado nível.
| Data | Altura da Maré (m) |
|---|---|
| 2022-12-01 00:00:00 | 3.22318 |
| 2022-12-03 00:00:00 | 2.63906 |
| 2022-12-04 00:00:00 | 2.70978 |
| 2022-12-05 00:00:00 | 3.32984 |
| 2022-12-07 00:00:00 | 3.21263 |
| 2022-12-20 00:00:00 | 3.46116 |
| 2022-12-24 00:00:00 | 2.80849 |
| 2022-12-25 00:00:00 | 2.69738 |
| 2022-12-30 00:00:00 | 2.99911 |
Veja que os intervalos de tempo entre os registros não são iguais.
Por exemplo, se você estiver registrando os carros que passam em frente à sua casa, o intervalo entre a passagem de um carro e outro não é constante.
Outro exemplo é o registro de defeitos numa linha de produção.
Os defeitos não acontecem sempre no mesmo intervalo, então a série temporal terá intervalos de tempo diferentes entre os registros.
Séries temporais regulares tendem a ser mais fáceis de modelar e prever, mas a irregularidade de uma série não é necessariamente um problema.
Quais São Os Componentes De Uma Série Temporal?
Séries temporais podem ser decompostas em 4 componentes principais: tendência, sazonalidade, ciclo e ruído.
Mas o que significa decompor uma série temporal?
Para entendermos melhor os valores da série, nós criamos algumas suposições sobre como ela é formada.
Uma suposição comum é que a série temporal é formada pela soma desses componentes (modelo aditivo).
Pensar em séries temporais como a soma de componentes vai te ajudar muito a entender melhor o que está acontecendo com os dados.
Decomposição Aditiva de Séries Temporais
Esta é a forma mais comum de decomposição de séries temporais.
Vamos continuar com o exemplo de uma série de temperaturas.
No modelo aditivo, vamos pensar que o valor final da temperatura que medimos em um momento do tempo é a soma de 4 componentes:
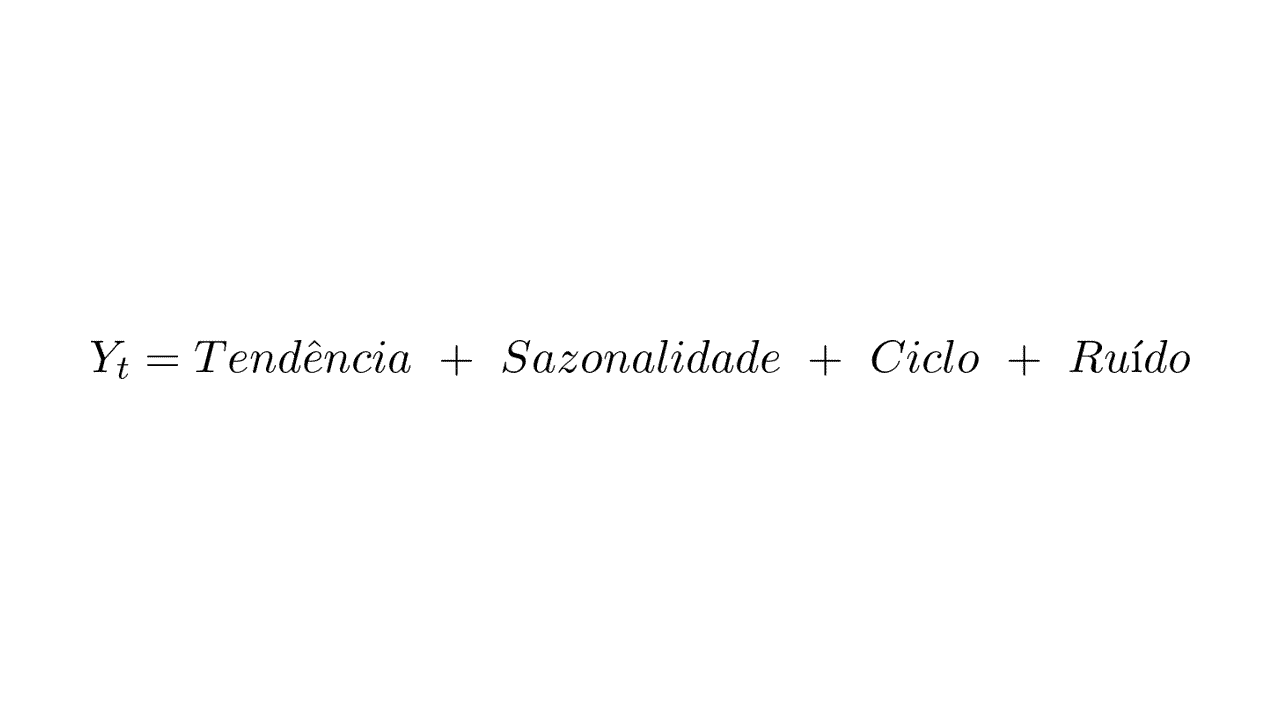
Onde Y_t é o valor da temperatura no tempo t.
Nem sempre você terá todos os componentes numa série temporal, mas vamos ver como cada um deles funciona.
Você pode ter séries que possuem apenas tendência, sazonalidade e ruído, por exemplo.
Tendência Em Séries Temporais
A tendência é a direção geral dos dados ao longo do tempo.
Por exemplo, com o aquecimento global a tendência é que a temperatura aumente com o passar do tempo.
Este componente modela esse aumento.
Se estivéssemos modelando a venda de jornais impressos, a tendência seria negativa, pois cada vez menos pessoas compram este produto.
Sazonalidade Em Séries Temporais
A sazonalidade é uma variação dos dados que sempre ocorre (se repete) em um período específico conhecido.
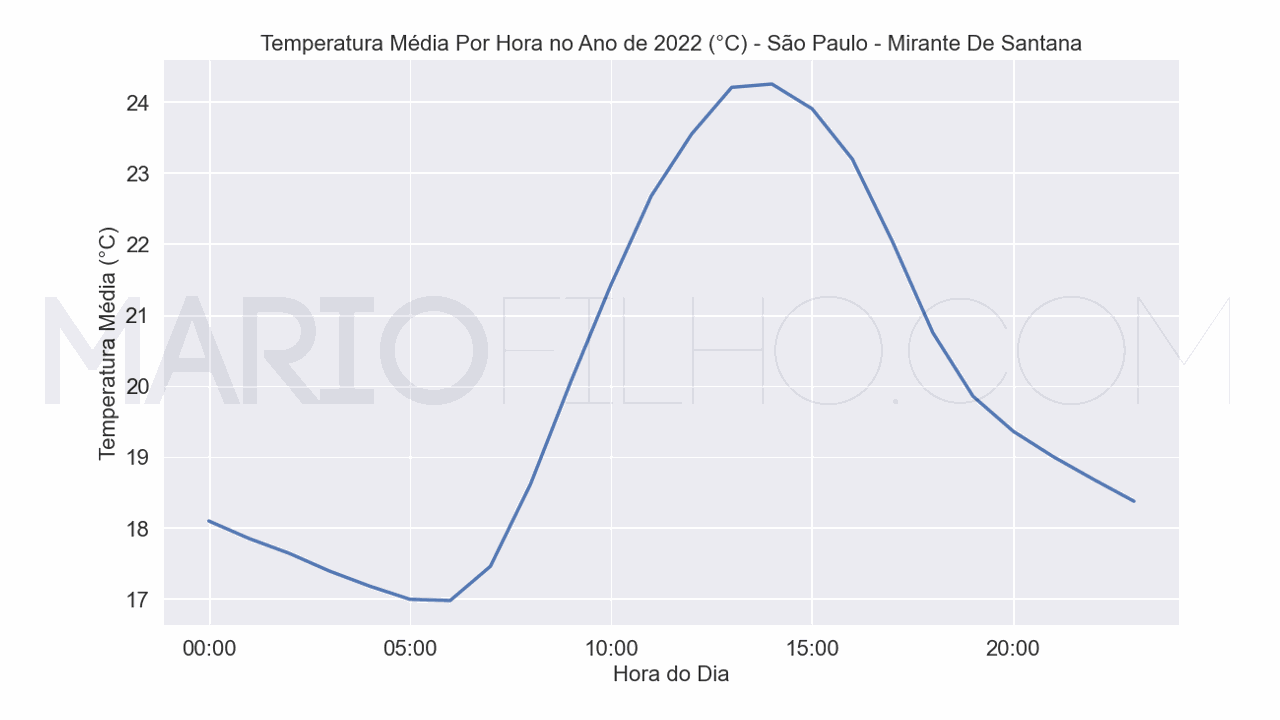
No gráfico acima você vê a sazonalidade diária na temperatura de São Paulo.
Temperaturas mais altas ocorrem durante o dia e mais baixas durante a noite.
Este efeito ocorre todos os dias nas mesmas horas, então entra na categoria de sazonalidade.
Outro exemplo é o aumento das vendas do varejo em datas comemorativas como Black Friday, Natal e Dia das Mães.
Ciclo Em Séries Temporais
Ciclo também é uma variação dos dados que ocorre em um período específico e se repete, mas não tem uma frequência fixa como nos exemplos da sazonalidade.
É muito fácil confundir sazonalidade e ciclo, mas lembre-se que o ciclo não vai acontecer sempre no mesmo período.
O exemplo mais comum é o ciclo econômico, que pode ser visto nas medidas de PIB e desemprego de um país.
Existem períodos de crescimento do PIB, com baixo desemprego, seguidos de períodos de recessão, com alta taxa de desemprego.
Ninguém sabe ao certo quando esses períodos vão acontecer, mas eles sempre acontecem.
Ruído Em Séries Temporais
O ruído é a variação aleatória dos dados que não pode ser explicada pelos outros componentes.
No exemplo da temperatura, temos a variação natural do equipamento de medição.
Por mais preciso que seja um termômetro, ele sempre terá uma margem de erro.
Isso fica muito claro se você tentar medir a temperatura no mesmo lugar com equipamentos diferentes.
Essa variação não é devida à tendência, sazonalidade ou ciclo, então ela é considerada ruído.
O Que É Lag Na Análise de Séries Temporais?
“Lag” é o deslocamento de um valor anterior de uma série para um período posterior.
Ele fica muito mais fácil de entender se pensarmos em como prever um valor futuro de uma série temporal.
Imagine que você trabalhe numa grande loja de varejo e seu chefe pediu que você fizesse uma previsão do faturamento da loja amanhã.
Uma previsão surpreendentemente boa e simples é usar o valor de faturamento de hoje como previsão para amanhã.
Neste caso, você estará usando o “lag” de 1 período como previsão, porque você terá deslocado o valor de hoje para amanhã.
Você também pode fazer isso com períodos maiores que 1.
Na tabela abaixo, usando nossos dados de temperatura, você pode ver colunas com o Lag 1 e Lag 3 da temperatura.
| Data | TEMPERATURA | LAG 1 TEMPERATURA | LAG 3 TEMPERATURA |
|---|---|---|---|
| 2022-12-27 00:00:00 | 23.0042 | 22.4458 | 21.05 |
| 2022-12-28 00:00:00 | 21.9417 | 23.0042 | 21.8042 |
| 2022-12-29 00:00:00 | 22.325 | 21.9417 | 22.4458 |
| 2022-12-30 00:00:00 | 21.5958 | 22.325 | 23.0042 |
| 2022-12-31 00:00:00 | 21.5083 | 21.5958 | 21.9417 |
Outra maneira muito eficaz de fazer essa previsão é considerar o valor de faturamento no mesmo dia da semana, só que na semana anterior.
Neste caso, você deslocará o valor de 7 dias atrás para hoje, usando então o “lag” de 7 períodos como previsão.
O Que é Autocorrelação Numa Série Temporal?
Autocorrelação é a medida da correlação entre uma série temporal e uma versão deslocada dela própria.
Em outras palavras, é a medida da similaridade entre os dados em diferentes pontos no tempo.
Por exemplo, se você correlacionar a temperatura de hoje com a temperatura de ontem, você verá que elas têm uma correlação positiva.
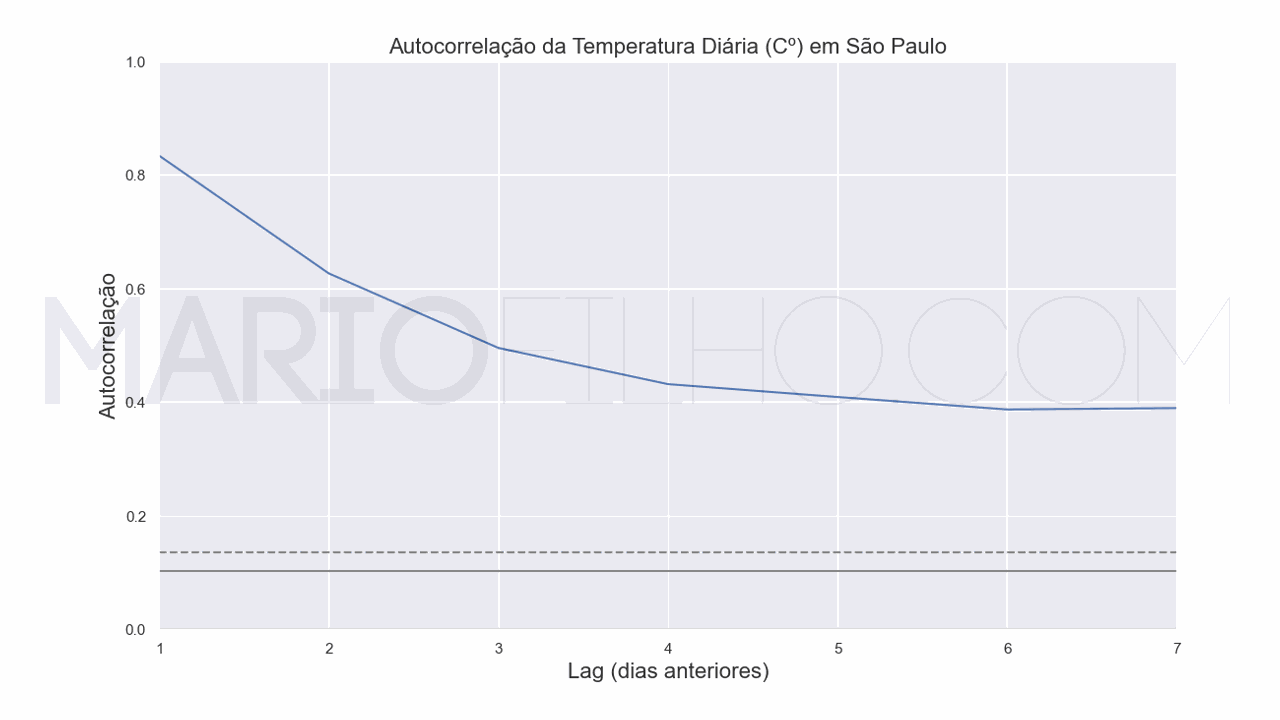
Ou seja, se a temperatura de ontem foi alta, a temperatura de hoje tende a ser alta também.
Lembrando que correlação não implica em causalidade: a temperatura de ontem não causou a temperatura de hoje, mas elas estão relacionadas.
No gráfico é possível ver que a autocorrelação mais alta é com o dia anterior (lag 1) e vai diminuindo conforme você compara com dias mais distantes.
Quando os dados são completamente aleatórios, ou seja, um valor não tem relação com o valor anterior, a autocorrelação é zero.
Um exemplo de autocorrelação bem próxima de zero é a correlação entre os retornos de dias consecutivos do Ibovespa.
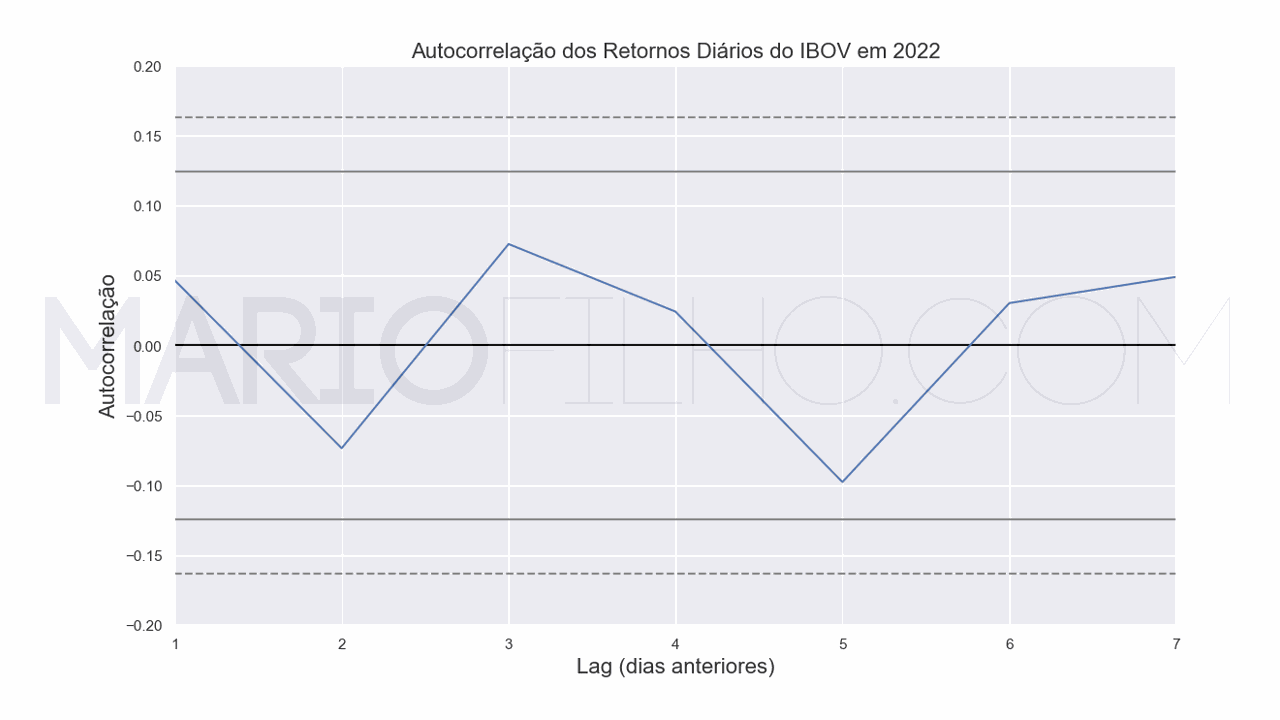
Preste atenção no eixo Y, que vai de -0.25 a 0.25 neste caso para mostrar melhor a autocorrelação.
As barras pretas indicam se a autocorrelação passa pelo crivo de significância estatística.
Ou seja, números entre elas indicam que a autocorrelação medida não é estatísticamente diferente de zero, só vemos desvios do zero por causa do ruído.
Em geral, o retorno de um dia não tem relação com o retorno do dia anterior.
Já no caso de autocorrelação negativa, podemos pensar numa série de exercícios físicos.
Se você correr 10km hoje, provavelmente amanhã você estará mais cansado e não vai conseguir correr tanto.
Quanto mais você corre em um dia (período anterior), menos você consegue correr no dia seguinte (período atual).
Como Machine Learning É Usado Com Séries Temporais?
Existem várias aplicações de machine learning sobre séries temporais.
Estes são alguns exemplos comuns:
Previsão de Séries Temporais
Essa é, de longe, a tarefa mais comum.
Modelos de machine learning são usados para analisar dados históricos de uma série temporal e fazer previsões sobre o comportamento futuro.
Alguns exemplos clássicos são:
- previsão de demanda por produtos para planejamento de estoque
- previsão de acessos diários a um site para planejamento de capacidade de servidores
- previsão de retornos de ações para composição de portfólio
Classificação de Séries Temporais
Modelos de machine learning também são usados para classificar séries temporais em diferentes categorias.
Um exemplo é avaliar séries de sinais de Eletrocardiograma (ECG) para detectar arritmias cardíacas.
Neste caso não queremos prever um ou mais períodos futuros de uma série específica, mas sim classificar a série completa de medições como normal ou anormal.
Detecção de Anomalias em Séries Temporais
Outro uso de machine learning é para identificar comportamentos incomuns em séries temporais, como picos ou quedas inesperadas.
Um exemplo da área de segurança é identificar picos incomuns no número de acessos a um site, já que isso pode indicar um ataque de negação de serviço (DDoS).
O modelo de machine learning pode processar milhões de séries temporais e entender, para cada uma, quais são os padrões normais e quais são os comportamentos anômalos.
Os dados usados neste artigo foram obtidos:
- na área de Dados Históricos do Portal INMET.
- no site TradingView
