Prever séries temporais é uma tarefa muito comum no dia a dia de um cientista de dados.
Seja prever a demanda futura de um produto, o tráfego de uma cidade ou até mesmo o clima.
Com previsões precisas de séries temporais, as empresas podem ajustar suas estratégias de produção, gerenciamento de estoque, alocação de recursos e outras decisões importantes, levando a uma redução significativa de custos e aumento da eficiência.
Além disso, as previsões também permitem que as empresas sejam mais proativas em vez de reativas, antecipando as tendências do mercado e ajustando suas estratégias em conformidade.
Neste artigo você aprenderá a fazer isso de forma muito fácil com o scikit-learn e a biblioteca mlforecast!
Índice
- Instalando a MLForecast e o Scikit-learn
- Como Preparar os Dados para o Modelo
- Feature Engineering Para Séries Temporais
- Conferindo a Computação das Features
- Método de Previsão Recursivo vs Direto
- Importância das Features
- Baseline Simples Com Sazonalidade
Instalando a MLForecast e o Scikit-learn
Em vez de perder tempo e correr o risco de cometer erros no preparo dos dados, vamos usar a biblioteca mlforecast.
Ela possui classes que transformam nossos dados brutos no formato correto para fazermos o treinamento e previsão com o scikit-learn.
Além disso ela computa as principais features de séries temporais para nós, como agregações de janelas móveis, lags, diferenças, etc.
Por fim, ela internaliza o loop de previsão recursiva para fazermos previsões para vários passos no futuro.
Vou explicar mais sobre tudo isso no decorrer do artigo.
Você pode instalar a biblioteca com o pip:
pip install mlforecast
pip install matplotlib
Ela já vai instalar o scikit-learn, numpy e pandas.
Vamos precisar também do matplotlib para visualizar os resultados.
Ela também possui uma versão no repositório do Anaconda, mas eu recomendo instalar a versão do pip, pois ela está mais atualizada.
Como Preparar os Dados para o Modelo
Vamos usar dados reais de vendas da rede de lojas Favorita, do Equador.
Temos dados de vendas de 2013 a 2017 para diversas lojas e categorias de produtos.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
path = 'train.csv'
data = pd.read_csv(path, index_col='id', parse_dates=['date'])
Para rodar o exemplo mais rápido, vamos usar apenas os dados de uma loja e duas categorias de produtos.
data2 = data.loc[(data['store_nbr'] == 1) & (data['family'].isin(['MEATS', 'PERSONAL CARE'])), ['date', 'family', 'sales', 'onpromotion']]
data2 = data2.rename(columns={'date': 'ds', 'sales': 'y', 'family': 'unique_id'})
As colunas são:
date: data do registrofamily: categoria do produtosales: número de vendasonpromotion: a quantidade de produtos daquela categoria que estavam em promoção naquele dia
Para manter o padrão das bibliotecas do grupo Nixtla, que é o criador da mlforecast, vamos renomear as colunas para ds (data), y (alvo) e unique_id (family).
O unique_id deve identificar cada série temporal que você tem.
No caso temos duas séries temporais, uma para cada categoria de produto.
Se tivéssemos mais de uma loja, teríamos que adicionar o número da loja junto com as categorias ao unique_id.
Um exemplo seria unique_id = store_nbr + '_' + family.
Este é o formato final do dataframe data2:
| ds | unique_id | y | onpromotion |
|---|---|---|---|
| 2013-01-01 00:00:00 | MEATS | 0 | 0 |
| 2013-01-01 00:00:00 | PERSONAL CARE | 0 | 0 |
| 2013-01-02 00:00:00 | MEATS | 369.101 | 0 |
| 2013-01-02 00:00:00 | PERSONAL CARE | 194 | 0 |
| 2013-01-03 00:00:00 | MEATS | 272.319 | 0 |
Uma linha para cada registro contendo a data, o ID da série temporal (categoria do produto em nosso exemplo), o valor da variável alvo e o valor de variáveis externas.
Veja que as séries temporais estão empilhadas.
Por fim vamos separar os dados de treino e validação.
Validação Temporal
Você jamais deve usar validação simples, aleatória ou k-fold para séries temporais.
Isso insere o que chamamos de vazamento de dados, pois você está usando dados futuros para treinar seu modelo.
Na prática você não teria esses dados no momento de fazer a previsão, então você não pode usá-los para treinar seu modelo.
Para evitar isso, vamos usar uma validação temporal simples entre passado e futuro.
Uma dica: saber fazer a validação temporal correta é uma habilidade que vai te diferenciar de muitos cientistas de dados (até mesmo experientes!).
Nossos dados de treino cobrirão os anos de 2013 a 2016 e os dados de validação serão os 3 primeiros meses de 2017.
train = data2.loc[data2['ds'] < '2017-01-01']
valid = data2.loc[(data2['ds'] >= '2017-01-01') & (data2['ds'] < '2017-04-01')]
Feature Engineering Para Séries Temporais
Agora que já temos os dados formatados de acordo com o que a mlforecast espera, vamos definir as features que vamos usar.
Essa parte é crucial para o sucesso de seu modelo.
Eu costumo pensar em 4 tipos de features principais para séries temporais:
Lags
Lags são simplesmente valores passados da série temporal que você inclui como features para o modelo.
Por exemplo, se você está tentando prever a demanda de um produto daqui a uma semana, pode incluir a demanda do mesmo dia da semana, mas na semana anterior como feature.
Na prática a demanda de um produto em um dia da semana acaba sendo similar em semanas diferentes, então essa feature pode ser útil para o modelo.
Você também pode criar lags mais longos, como o valor da série temporal no mesmo dia do ano anterior (imagine que você está tentando prever a demanda de um produto no Natal ou Black Friday).
É importante testar vários valores de lags para encontrar o que funciona melhor para o seu problema específico.
Ninguém pode te dizer quais são os melhores lags para o seu problema sem testar.
Agregações Temporais
As agregações temporais são operações aplicadas a uma janela de observações da série temporal.
Por exemplo, calcular a média de vendas diárias dos últimos 7 dias, ou o desvio padrão dos retornos de um ativo financeiro nas últimas 4 semanas.
Essas agregações podem ajudar o modelo a identificar tendências e padrões na série temporal.
Assim como no caso dos lags, é importante experimentar várias agregações temporais e vários tamanhos de janelas diferentes, para encontrar o que funciona melhor para o seu problema específico.
Componentes da Data
Os componentes da data são valores que você extrai de uma data ou hora específica.
Por exemplo, você pode incluir a hora do dia, o dia da semana, o mês, a estação do ano, etc.
Essas features podem ajudar o modelo a identificar padrões sazonais e cíclicos na série temporal.
Preciso dizer que é importante testar vários componentes de data diferentes para encontrar o que funciona melhor para o seu problema específico?
Diferenças
As diferenças são o resultado da subtração entre valores da série temporal.
Por exemplo, você pode incluir a diferença entre a demanda de hoje e a demanda de ontem.
Mesmo com os lags, as diferenças podem trazer informações mais detalhadas para o modeo e ajudá-lo a identificar os padrões com mais facilidade.
A mesma recomendação de testar “diferenças diferentes” 🙂 vale aqui.
Código Para Feature Engineering
Agora que já sabemos quais features vamos usar, vamos criar uma função para aplicar essas features em nossos dados.
Antes disso, precisamos criar uma lista com os modelos do scikit-learn que queremos testar.
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor
models = [RandomForestRegressor(random_state=0, n_estimators=100),
ExtraTreesRegressor(random_state=0, n_estimators=100)]
Vamos testar apenas 2 modelos, a Random Forest e a Extra Trees, mas você pode testar quantos modelos quiser. Basta importá-los e adicionar à lista com os argumentos que você quiser.
A mlforecast e a biblioteca window_ops que são usadas para computar as features não possuem suporte para calcular as features de diferença, por isso precisei criar a função diff usando o numba.
from numba import njit
@njit
def diff(x, lag):
x2 = np.full_like(x, np.nan)
for i in range(lag, len(x)):
x2[i] = x[i] - x[i-lag]
return x2
numba é uma biblioteca que otimiza seu código Python para rodar mais rápido e é recomendando pelos desenvolvedores da mlforecast na hora de criar funções para computar features.
No caso precisamos usar o decorator @njit para que a função seja compilada pelo numba.
A função recebe dois argumentos, x e lag. x é uma array e lag é o número de períodos que você quer usar para calcular a diferença.
A primeira linha dentro da função cria uma nova array x2 com o mesmo formato que a array x, mas todos os valores são inicializados como NaN.
Dentro do loop, o valor na posição i da array x2 é a diferença entre o valor na posição i e o valor i-lag da array original.
Se for um lag de 3 períodos, por exemplo, o valor na posição 3 da array x2 é a diferença entre o valor original da série temporal nessa posição e o valor na posição 0.
Por fim, a função retorna a array com as diferenças calculadas.
Agora vamos criar o objeto que gerencia a criação das features e o treinamento dos modelos.
from window_ops import rolling_mean
from mlforecast import MLForecast
model = MLForecast(models=models,
freq='D',
lags=[1,7,14],
lag_transforms={
1: [(rolling_mean, 3), (rolling_mean, 7), (rolling_mean, 28), (diff, 1), (diff, 7)], # aplicado a uma janela W a partir do registro Lag
},
date_features=['dayofweek'],
num_threads=6)
O objeto que vai facilitar o nosso trabalho é o MLForecast.
Ele é o objeto responsável por aplicar as transformações e treinar os modelos.
No primeiro argumento, passamos a lista de modelos que queremos treinar, conforme definido anteriormente.
A segunda linha, freq='D', indica que a frequência da série temporal é diária.
O terceiro argumento, lags=[1,7,14], indica os valores de lag que queremos usar como features. Neste caso, serão usados os lags de 1, 7 e 14 dias.
No argumento lag_transforms={...}, passamos um dicionário com as transformações mais complexas que queremos aplicar à série, como agregações temporais e diferenças.
Neste caso, vamos calcular uma média móvel de 3, 7 e 28 dias e a diferença entre o valor atual e o valor de 1 e 7 dias atrás.
Lembrando que o “valor atual” não é o alvo da data atual (já que esse é o valor que queremos prever), mas sim o valor da data do lag indicado.
As funções recebem a série temporal modificada pelo lag com as observações na mesma ordem do dataframe original (geralmente do registro mais antigo para o mais recente).
Nesse caso, por exemplo, é a média móvel de 7 dias a partir do registro de lag 1, e assim vai.
No argumento date_features=['dayofweek'] especificamos quais componentes da data ele deve extrair. Neste caso, vamos usar apenas o dia da semana.
Por fim, o argumento num_threads=6 especifica quantas threads devem ser usadas para processar os dados em paralelo.
Meu computador tem 6 núcleos, então usei 6 threads. Se você tiver um computador com mais núcleos, pode usar mais threads.
Lembrando que além dessas features temos a onpromotion, que é uma variável externa relacionada ao alvo.
Ela será usada durante o treinamento e na hora de fazer as previsões assim como qualquer outra coluna que você tiver no dataframe de treino que não seja data, alvo ou ID.
Caso você tenha features estáticas (que não variam com o tempo), como o código do produto, você pode passar uma lista com os nomes delas no argumento static_features do método fit.
Mesmo não tendo essas features, é importante passar uma lista vazia para esse argumento, pois o MLForecast considera as outras variáveis externas como features estáticas caso você não faça isso.
model.fit(train, id_col='unique_id', time_col='ds', target_col='y', static_features=[])
p = model.predict(horizon=90, dynamic_dfs=[valid[['unique_id', 'ds', 'onpromotion']]])
p = p.merge(valid[['unique_id', 'ds', 'y']], on=['unique_id', 'ds'], how='left')
No método fit, passamos o dataframe de treino, os nomes das colunas com o ID das séries temporais, data e alvo e a lista de features estáticas.
No método predict, passamos o horizonte de previsão horizon que é o número de períodos que queremos prever contados a partir da última data do dataframe de treino.
Como usamos variáveis externas dinâmicas, precisamos passar um dataframe com os valores delas para os períodos que queremos prever.
No nosso caso podemos planejar quais produtos entrarão em promoção nos próximos 90 dias ou até simular as vendas para definir as promoções que devemos fazer.
No caso de variáveis externas como temperatura, precisamos usar estimativas para os próximos períodos, o que pode prejudicar a qualidade das previsões.
Um erro comum é usar os valores históricos das variáveis externas durante a validação sem considerar que elas não estarão disponíveis no momento da previsão em produção.
Isso te dará uma estimativa muito otimista do desempenho do modelo, que não vai se manter na prática.
Por isso é importante testar o modelo usando o mesmo processo de geração das variáveis externas que será usado em produção.
As variáveis externas são passadas numa lista de dataframes no argumento dynamic_dfs.
É importante que os dataframes com as variáveis externas tenham colunas que indiquem a data do registro e potencialmente o ID da série temporal para que o MLForecast possa fazer o join com o restante dos dados.
No caso da temperatura novamente, se tivéssemos o código do município como feature estática, passaríamos um dataframe com o código do município, data e a respectiva temperatura estimada.
Por fim fiz o merge com o dataframe de validação para facilitar o cálculo do erro e a visualização dos resultados.
As previsões de cada modelo são armazenadas em colunas com o nome do modelo.
| unique_id | ds | RandomForestRegressor | ExtraTreesRegressor | y |
|---|---|---|---|---|
| MEATS | 2017-01-01 00:00:00 | 121.464 | 122.198 | 0 |
| MEATS | 2017-01-02 00:00:00 | 116.526 | 256.113 | 116.724 |
| MEATS | 2017-01-03 00:00:00 | 234.785 | 281.266 | 344.583 |
| MEATS | 2017-01-04 00:00:00 | 277.051 | 257.225 | 326.203 |
| MEATS | 2017-01-05 00:00:00 | 277.553 | 243.968 | 274.205 |
Conferindo a Computação das Features
É importante verificar se as features foram computadas corretamente, sem problemas de vazamento de dados (como usar o alvo para computar uma média).
Para isso podemos usar o método preprocess que retorna um dataframe com as features computadas.
model.preprocess(train, id_col='unique_id', time_col='ds', target_col='y', static_features=[])
| ds | unique_id | y | onpromotion | lag1 | lag7 | lag14 | rolling_mean_lag1_window_size3 | rolling_mean_lag1_window_size7 | rolling_mean_lag1_window_size28 | diff_lag1_lag1 | diff_lag1_lag7 | dayofweek |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2013-01-29 00:00:00 | MEATS | 260.633 | 0 | 325.072 | 274.261 | 287.346 | 289.11 | 311.035 | 296.329 | 57.256 | 50.186 | 1 |
| 2013-01-29 00:00:00 | PERSONAL CARE | 91 | 0 | 107 | 90 | 95 | 88.6667 | 88.7143 | 98.5357 | 65 | 18 | 1 |
| 2013-01-30 00:00:00 | MEATS | 304.018 | 0 | 260.633 | 312.199 | 369.492 | 284.507 | 309.088 | 305.637 | -64.439 | -13.628 | 2 |
| 2013-01-30 00:00:00 | PERSONAL CARE | 98 | 0 | 91 | 103 | 118 | 80 | 88.8571 | 101.786 | -16 | 1 | 2 |
| 2013-01-31 00:00:00 | MEATS | 264.937 | 0 | 304.018 | 215.607 | 280.879 | 296.574 | 307.92 | 303.313 | 43.385 | -8.181 | 3 |
Escolha alguns exemplos e calcule manualmente os valores das features na série original para conferir se os valores computados pela MLForecast estão corretos.
Método de Previsão Recursivo vs Direto
Existem pelo menos 3 maneiras diferentes de gerar previsões quando você usa machine learning para séries temporais.
A maneira padrão da MLForecast é usar o método recursivo ou auto-regressivo.
Para entender esse método, imagine uma série temporal com apenas 10 observações e um modelo treinado para prever apenas 1 passo à frente.
Para obter a previsão para múltiplos períodos, vamos integrar essa previsão à série original, como se ela fosse uma nova observação e usar o modelo para prever o próximo período.
Faremos esse mesmo processo para os próximos períodos até que tenhamos previsões para todos os períodos que queremos.
Como alternativa, podemos usar o método direto, que treina um modelo para cada período que queremos prever.
Então se quisermos prever 10 períodos, treinamos 10 modelos, cada um para prever um período específico.
O método recursivo é mais rápido de treinar, principalmente se você tem um horizonte de previsão grande.
Não tem como saber qual método é melhor sem testar, então se você precisa da melhor performance, mesmo que o custo computacional seja alto, teste os dois.
Para usar o método direto no MLForecast, basta passar o argumento max_horizon no método fit com o número de períodos que você quer prever.
model.fit(train, id_col='unique_id', time_col='ds', target_col='y',
static_features=[], max_horizon=90)
Importância das Features
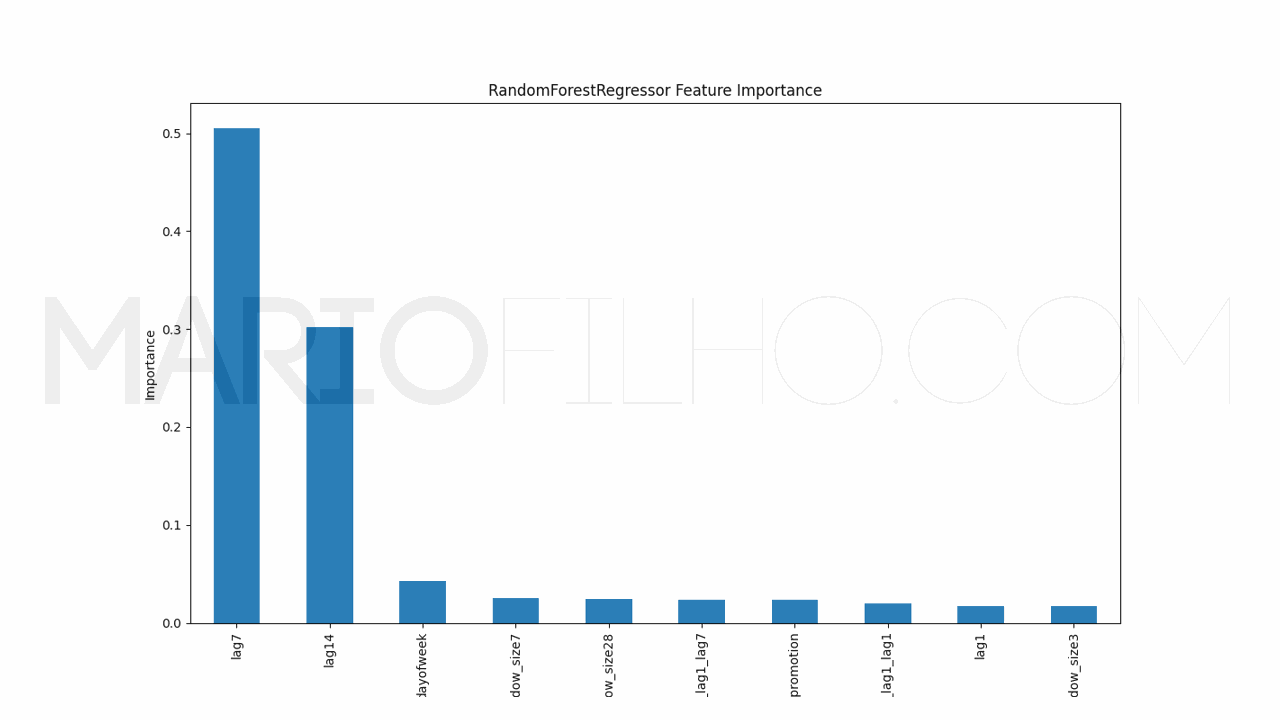
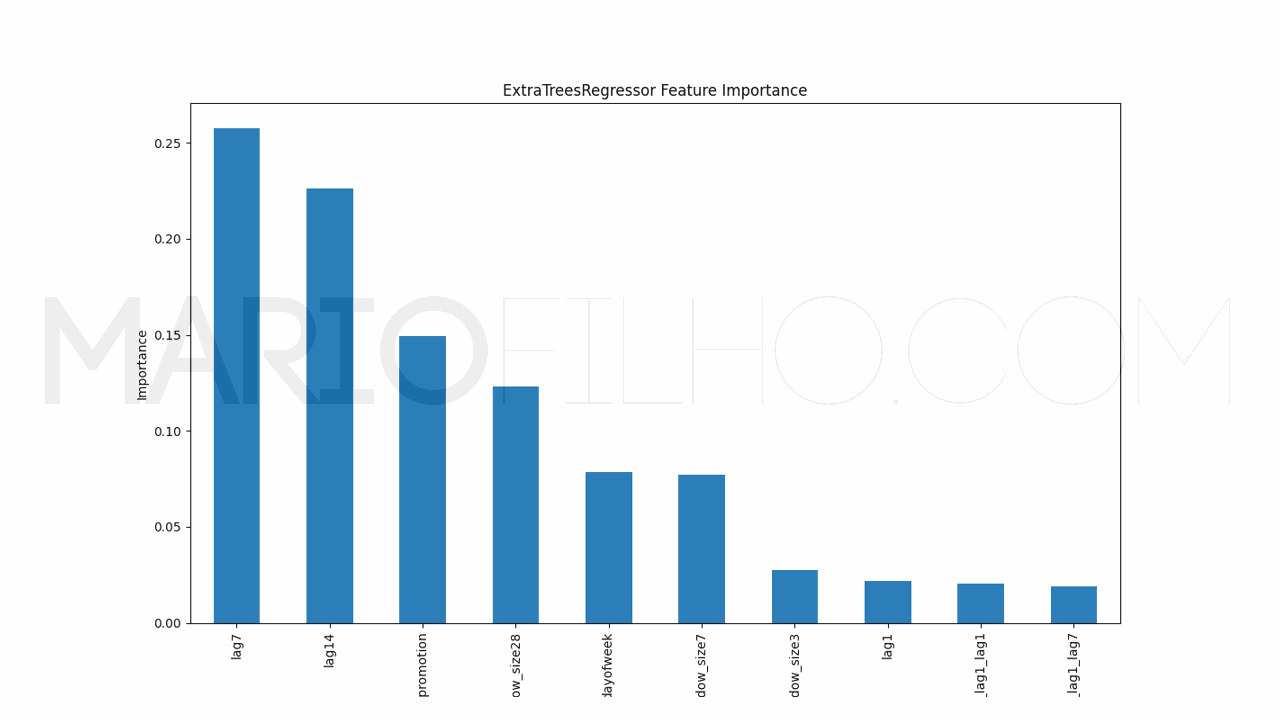
Para entender como o modelo está tomando suas decisões, podemos usar o cálculo interno de importância das features.
É muito simples extraí-las usando o atributo feature_importances_ do modelo.
pd.Series(model.models_['RandomForestRegressor'].feature_importances_, index=model.ts.features_order_).sort_values(ascending=False).plot.bar(
figsize=(1280/96,720/96), title='RandomForestRegressor Feature Importance', xlabel='Features', ylabel='Importance')
Neste caso veremos um gráfico de barras com as features no eixo X e sua importância no eixo Y. Quanto maior a barra, mais o modelo considera esta feature na hora de gerar a previsão.
Como Calcular o Erro da Previsão
Por fim, podemos calcular o erro usando a métrica que quisermos como já fazemos no scikit-learn normalmente.
Criei uma função para calcular o WMAPE, que é uma adaptação do erro percentual que resolve o problema de dividir por zero.
O peso de cada amostra, neste caso, é dado pela magnitude do valor real.
O código com a fórmula simplificada fica:
def wmape(y_true, y_pred):
return np.abs(y_true - y_pred).sum() / np.abs(y_true).sum()
print(f"WMAPE RandomForestRegressor: {wmape(p['y'], p['RandomForestRegressor'])}\nWMAPE ExtraTreesRegressor: {wmape(p['y'], p['ExtraTreesRegressor'])}")
Neste caso o erro da RandomForestRegressor foi de 19,38% e o da ExtraTreesRegressor foi de 18,49%.
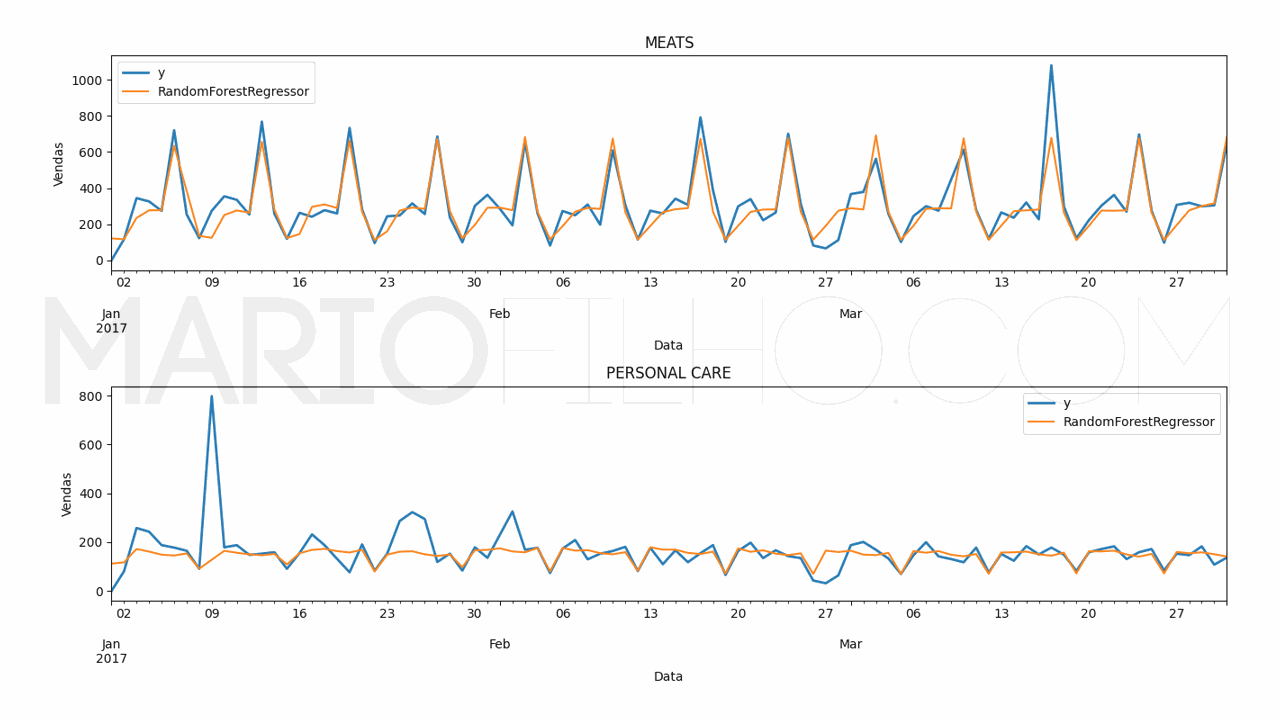
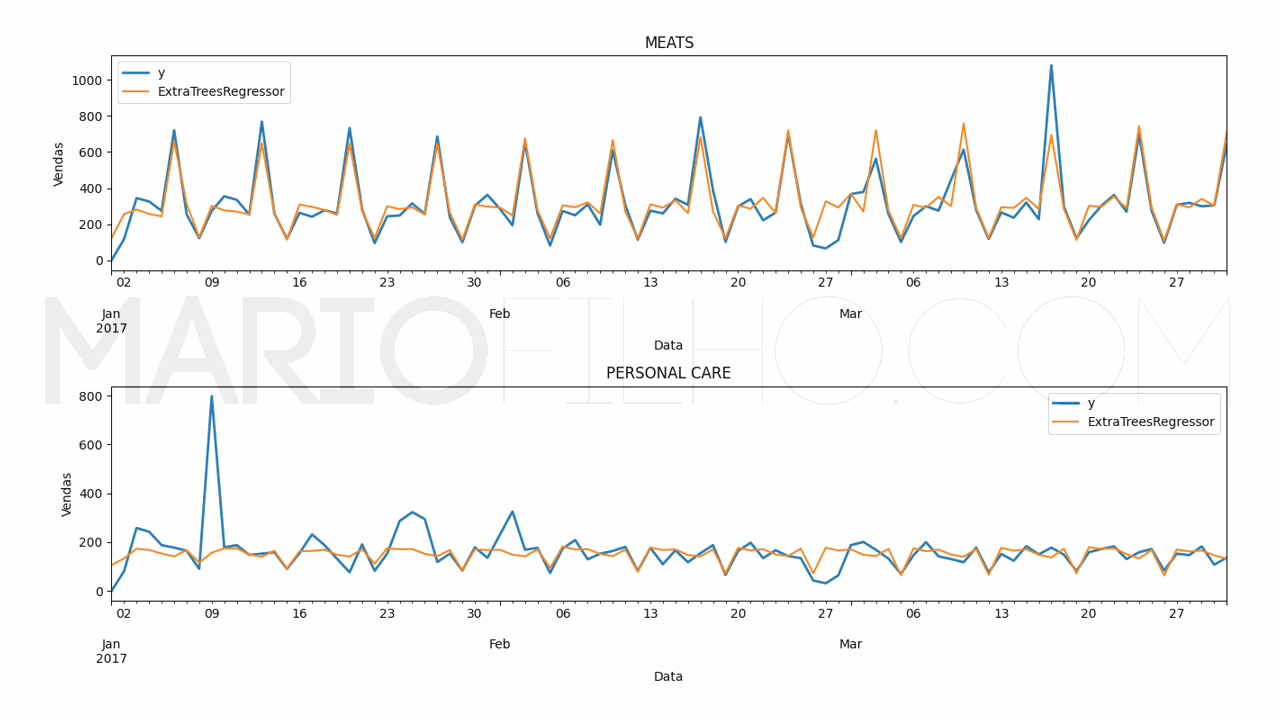
O código para fazer os gráficos ficou assim:
for model in ['RandomForestRegressor', 'ExtraTreesRegressor']:
fig,ax = plt.subplots(2,1, figsize=(1280/96, 720/96))
for ax_, family in enumerate(['MEATS', 'PERSONAL CARE']):
p.loc[p['unique_id'] == family].plot(x='ds', y='y', ax=ax[ax_], label='y', title=family, linewidth=2)
p.loc[p['unique_id'] == family].plot(x='ds', y=model, ax=ax[ax_], label=model)
ax[ax_].set_xlabel('Data')
ax[ax_].set_ylabel('Vendas')
fig.tight_layout()
Baseline Simples Com Sazonalidade
Para saber se vale a pena colocar um modelo mais complexo em produção, é importante ter uma baseline simples para comparar.
Ela pode ser a solução atual usada em sua empresa ou uma solução simples como a média dos valores passados no mesmo período.
Vamos usar a baseline de sazonalidade, que é uma técnica simples que usa a média dos valores passados no mesmo período do ano.
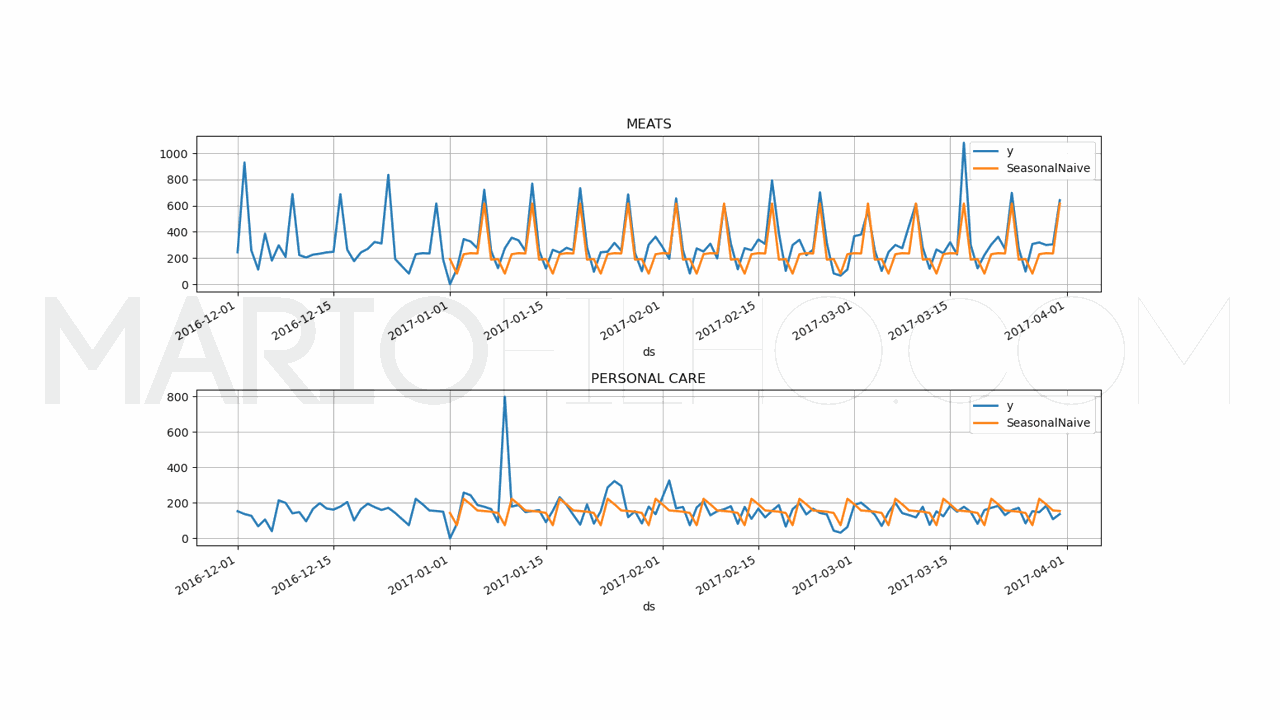
Esta baseline possui um WMAPE de 31,53% no mesmo período.
Neste caso, ambos os modelos de machine learning tiveram um desempenho melhor, o que os deixa um passo mais perto de serem colocados em produção.
Visite este artigo para ver como calcular essa baseline.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.