A modelagem de séries temporais com deep learning (redes neurais) é uma área em constante evolução.
Falar de “redes neurais” pode se referir a vários tipos diferentes de técnicas como redes neurais convolucionais, redes neurais recorrentes, redes neurais tradicionais (MLP) e redes neurais com mecanismo de atenção (transformer).
Por isso, primeiro vou te dar uma visão geral dessas técnicas, indicando artigos mais detalhados sobre cada uma e depois vou te mostrar como aplicar uma rede neural tradicional (MLP) para prever séries temporais.
Não subestime essa arquitetura mais simples!
Já perdi competições porque insisti em testar redes neurais mais complexas enquanto os vencedores usavam redes neurais tradicionais.
Índice
- Tipos de Redes Neurais Para Séries Temporais
- Como Instalar a NeuralForecast Com e Sem Suporte a GPU
- Como Preparar a Série Temporal Para Redes Neurais
- Hiperparâmetros e Arquitetura da Rede Neural
- Treinamento da Rede Neural
- Como Adicionar Variáveis Externas à Rede Neural
- Baseline Simples Com Sazonalidade
- Loss Function Personalizada com PyTorch (WMAPE)
Tipos de Redes Neurais Para Séries Temporais
Redes Neurais Recorrentes (LSTM e GRU)
As redes neurais recorrentes (RNNs) são uma classe de redes neurais criadas especialmente para lidar com dados sequenciais.
Elas são estruturadas para manter uma espécie de memória de informações vistas e usar essas informações para prever o próximo ponto de dados.
Uma analogia para entender como as RNNs funcionam é pensar em como você assiste uma série de TV, como Game of Thrones.
Cada episódio representa uma etapa no tempo e você mantém uma representação mental dos episódios anteriores para ajudá-lo a entender o próximo.
Da mesma forma, uma RNN lê cada ponto de dados em uma série temporal, atualiza sua representação interna e usa tudo isso para ajudar a prever a próxima observação.
Uma das variações mais populares de RNN é a LSTM (Long Short-Term Memory), que foi projetada para lidar melhor com problemas em que a dependência temporal é muito longa.
Na nossa analogia, é a ideia de precisar lembrar de alguma coisa da primeira temporada para entender o que está acontecendo na última.
Em resumo, as RNNs e sua variação LSTM são uma ótima opção para previsão de séries temporais devido à sua estrutura especial para lidar com dados sequenciais.
Leia este artigo para aprender a prever séries temporais com LSTM em Python.
No entanto, assim como com qualquer outra técnica de modelagem, elas nem sempre serão a melhor opção.
É preciso testar e ver qual técnica funciona melhor em seus dados específicos.
Por isso é importante ter várias opções em sua caixa de ferramentas.
Redes Neurais Convolucionais (CNNs)
Apesar de serem muito populares por causa de seu desempenho em tarefas de visão computacional, as redes neurais convolucionais também podem ser usadas para prever séries temporais.
Elas têm um desempenho competitivo com as RNNs e são mais simples e rápidas de treinar.
Imagine uma CNN como um microscópio para séries temporais.
Quando estudamos um objeto através de um microscópio, nós o colocamos em uma lâmina e o passamos por uma série de lentes.
Cada lente amplia a imagem um pouco mais, permitindo que nós vejamos detalhes cada vez mais precisos.
Da mesma forma, os filtros da CNN focam em pequenos pedaços da série temporal, permitindo que a rede identifique características importantes para o alvo que você quer prever.
Leia este artigo para aprender a prever séries temporais com CNNs em Python.
Redes Neurais com Mecanismo de Atenção (Transformers)
Os transformers são uma classe de modelos de deep learning desenvolvidos inicialmente para o processamento de linguagem natural, mas que têm se mostrado eficazes em muitas outras tarefas envolvendo sequências, incluindo a previsão de séries temporais.
Se você parar para pensar, um texto é uma sequência de palavras ou caracteres, então devido ao imenso sucesso dos Transformers em NLP, é natural testá-los para outros tipos de dados sequenciais.
Os transformers permitem que a rede preste atenção e dê pesos diferentes às observações e variáveis adicionais da série temporal de acordo com as características da cada amostra específica que queremos prever.
Imagine que uma loja tem várias filiais em lugares diferentes do Brasil.
Se estivermos prevendo vendas em um shopping, podemos dar mais atenção às informações relacionadas aos fins de semana e feriados, enquanto que se estivermos prevendo vendas em uma loja de rua, voltamos a atenção às informações relacionadas aos horários de pico.
A diferença mais notável com relação às redes recorrentes é que os Transformers não precisam de uma memória interna para manter informações, eles conseguem adaptar o peso das informações da rede neural de acordo com o contexto.
Uma analogia que pode ajudar para entender o mecanismo de atenção nos Transformers é imaginar um grupo de médicos reunidos para discutir casos de pacientes internados em um hospital.
Para um paciente com arritmia cardíaca, o cardiologista terá uma opinião mais relevant (maior peso), já para um paciente com pneumonia, o pneumologista terá uma opinião mais relevante.
Apesar de alguns especialistas contribuirem mais para cada caso específico, todos os médicos se comunicam e trocam informações para chegar a um diagnóstico mais preciso.
Transformers são “famintos” por dados, então eles tendem a ir melhor quando você tem uma grande quantidade de dados para treinamento.
De qualquer maneira, eles também são uma ferramenta importante para ter na sua caixa de ferramentas.
Leia este artigo para aprender a prever séries temporais com Transformers em Python.
Redes Neurais Tradicionais (MLP)
As redes neurais tradicionais que a gente aprende em qualquer curso para iniciantes em machine learning também podem ser usadas para prever séries temporais.
Alguns nomes que você vai encontrar para elas são: MLP (Multi-Layer Perceptron), Rede Neural Feed-Forward e Fully-Connected.
Elas são compostas pelas camadas de entrada, saída e uma ou mais camadas ocultas de neurônios.
Cada uma conectada a todos os neurônios da camada anterior (por isso fully-connected).
A última camada (camada de saída) é responsável por retornar a previsão.
Existem arquiteturas mais complexas que tentam melhorar as previsões usando apenas camadas simples de maneira mais inteligente do que simplesmente conectando-as sequencialmente, como a NBEATS.
Como venho falando, não subestime essa arquitetura simples, porque ela pode ser melhor do que as arquiteturas complexas em problemas com poucos dados ou muito ruído.
Neste artigo, você vai aprender a usar essas redes neurais tradicionais para prever séries temporais.
Vamos usar a biblioteca NeuralForecast.
Como Instalar a NeuralForecast Com e Sem Suporte a GPU
Por usar métodos de redes neurais, se você tiver uma GPU, é importante ter o CUDA instalado para que os modelos rodem mais rápido.
Para verificar se você tem uma GPU instalada e configurada corretamente com PyTorch (backend da biblioteca), execute o código abaixo:
import torch
print(torch.cuda.is_available())
Esta função retorna True se você tem uma GPU instalada e configurada corretamente, e False caso contrário.
Caso você tenha uma GPU, mas não tenha o PyTorch instalado com suporte a ela, veja no site oficial como instalar a versão correta.
Recomendo que você instale o PyTorch primeiro!
O comando que usei para instalar o PyTorch com suporte a GPU foi:
conda install pytorch pytorch-cuda=11.7 -c pytorch -c nvidia
Se você não tem uma GPU, não se preocupe, a biblioteca funciona normalmente, só não fica tão rápida.
Instalar essa biblioteca é muito simples, basta executar o comando abaixo:
pip install neuralforecast
ou se você usa o Anaconda:
conda install -c conda-forge neuralforecast
Como Preparar a Série Temporal Para Redes Neurais
Vamos usar dados reais de vendas da rede de lojas Favorita, do Equador.
Temos dados de vendas de 2013 a 2017 para diversas lojas e categorias de produtos.
Nossos dados de treino cobrirão os anos 2013 a 2016 e os dados de validação serão os 3 primeiros meses de 2017.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
def wmape(y_true, y_pred):
return np.abs(y_true - y_pred).sum() / np.abs(y_true).sum()
Para medir o desempenho do modelo, vamos usar a métrica WMAPE (Weighted Mean Absolute Percentage Error).
Ela é uma adaptação do erro percentual que resolve o problema de dividir por zero.
data = pd.read_csv('train.csv', index_col='id', parse_dates=['date'])
data2 = data.loc[(data['store_nbr'] == 1) & (data['family'].isin(['MEATS', 'PERSONAL CARE'])), ['date', 'family', 'sales', 'onpromotion']]
Para simplificar, vamos usar apenas os dados de uma loja e duas categorias de produto.
As colunas são:
date: data do registrofamily: categoria do produtosales: número de vendasonpromotion: a quantidade de produtos daquela categoria que estavam em promoção naquele dia
weekday = pd.get_dummies(data2['date'].dt.weekday)
weekday.columns = ['weekday_' + str(i) for i in range(weekday.shape[1])]
data2 = pd.concat([data2, weekday], axis=1)
Além das vendas e indicador de promoções, vamos criar variáveis adicionais do dia da semana.
O dia da semana pode ser tratado como uma variável ordinal ou categórica, mas aqui vou usar a abordagem categórica que é mais comum.
Em geral, usar informações adicionais que sejam relevantes para o problema pode melhorar o desempenho do modelo.
Variáveis específicas da estrutura temporal, como dias da semana, meses, dias do mês são importantes para capturar padrões sazonais.
Existe uma infinidade de outras informações que poderíamos adicionar, como a temperatura, chuva, feriados, etc.
Nem sempre essas informações vão melhorar o modelo, e podem até piorar o desempenho, então sempre verifique se elas melhoram o erro nos dados de validação.
data2 = data2.rename(columns={'date': 'ds', 'sales': 'y', 'family': 'unique_id'})
A biblioteca neuralforecast espera que as colunas sejam nomeadas dessa forma:
ds: data do registroy: variável alvo (número de vendas)unique_id: identificador único da série temporal (categoria do produto)
O unique_id pode ser qualquer identificador que separe suas séries temporais.
Se quiséssemos modelar a previsão de vendas de todas as lojas, poderíamos usar o store_nbr junto com a family como identificadores.
train = data2.loc[data2['ds'] < '2017-01-01']
valid = data2.loc[(data2['ds'] >= '2017-01-01') & (data2['ds'] < '2017-04-01')]
h = valid['ds'].nunique()
Este é o formato final da tabela:
| ds | unique_id | y | onpromotion | weekday_0 | weekday_1 | weekday_2 | weekday_3 | weekday_4 | weekday_5 | weekday_6 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2013-01-01 00:00:00 | MEATS | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2013-01-01 00:00:00 | PERSONAL CARE | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2013-01-02 00:00:00 | MEATS | 369.101 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
Separamos os dados em treino e validação com uma divisão temporal simples entre passado e futuro.
A variável h é o horizonte, o número de períodos que queremos prever no futuro.
Neste caso, é o número de datas únicas na validação (90).
Vamos para a modelagem.
Hiperparâmetros e Arquitetura da Rede Neural
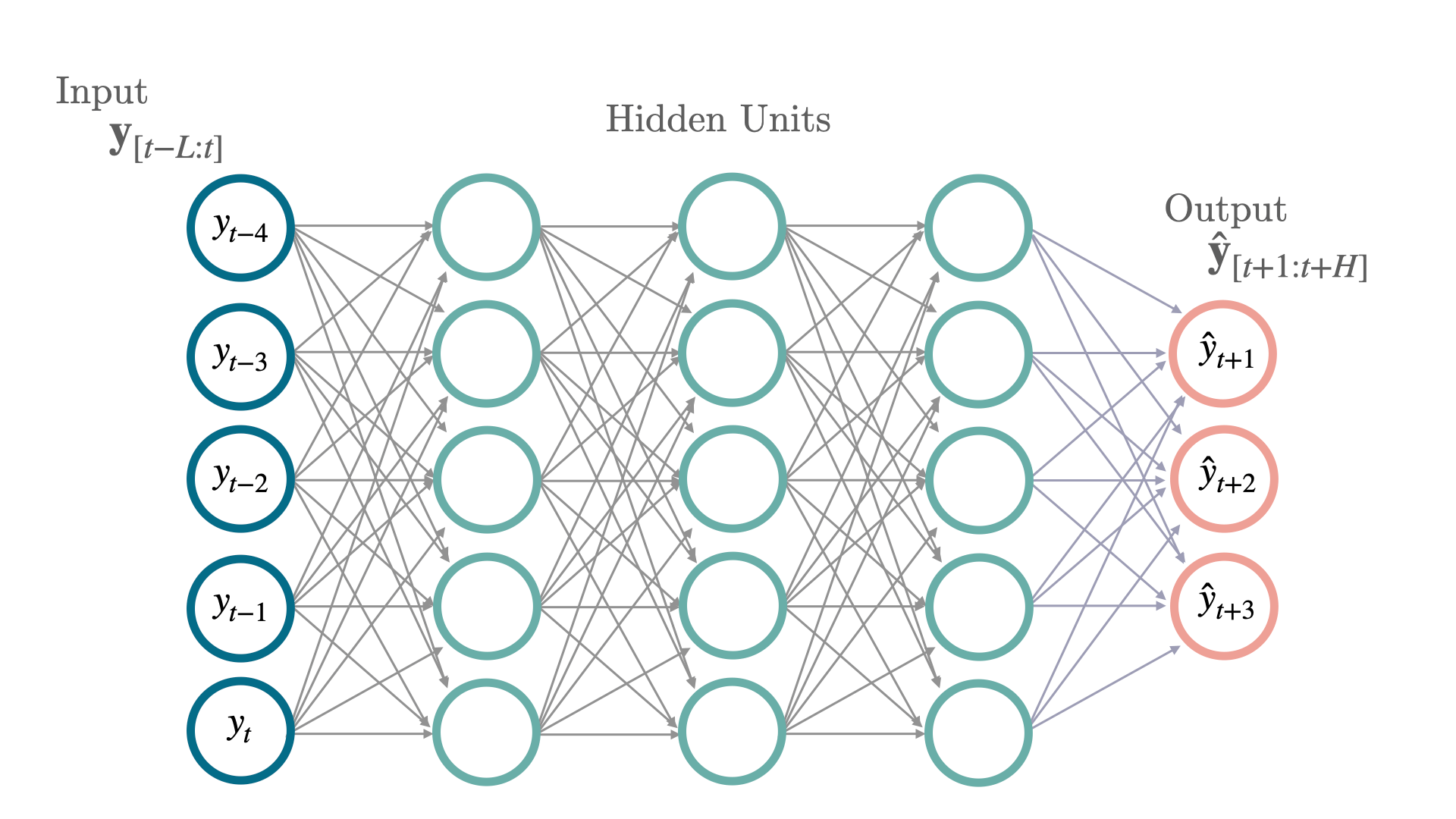 Fonte: https://nixtla.github.io/neuralforecast/models.mlp.html
Fonte: https://nixtla.github.io/neuralforecast/models.mlp.html
Vamos usar o objeto AutoMLP da biblioteca neuralforecast para fazer a busca automática dos melhores hiperparâmetros e treinar a rede neural.
É praticamente impossível saber quais são os melhores hiperparâmetros para uma rede neural em dados específicos sem testar vários valores.
Se alguém te disser que sabe fazer isso, é mentira!
Por isso precisamos testar várias combinações, mas em vez de fazer isso manualmente, vamos usar uma estratégia automática como a busca aleatória.
A busca aleatória se mostrou superior até mesmo a especialistas humanos e, junto com a otimização bayesiana, é uma das minhas estratégias favoritas para otimização de hiperparâmetros.
Você pode determinar os intervalos de busca para cada hiperparâmetro, mas eu recomendo usar os valores padrão, principalmente se você não tem muita experiência com redes neurais.
Depois você pode estudar as combinações para desenvolver sua intuição sobre como cada hiperparâmetro afeta o modelo.
Os hiperparâmetros e intervalos padrão são:
input_size_multiplier
Este hiperparâmetro é multiplicado pelo horizonte h para determinar o número de observações que serão usadas como entrada (features) para prever os próximos períodos.
Por exemplo, no nosso caso de previsão diária, se o horizonte for 90 e o input_size_multiplier for 2, as vendas para os últimos 180 dias serão usadas como features para prever os próximos 90 dias.
O intervalo padrão é de números inteiros de 1 a 5.
hidden_size
Este é o número de unidades (neurônios) em cada camada oculta da rede neural.
Ele determina parcialmente a capacidade do modelo de aprender padrões complexos nos dados.
O intervalo padrão é uma escolha entre 256, 512 e 1024.
Esses números geralmente são múltiplos de 2 porque as GPUs (placas de vídeo) são mais eficientes para fazer cálculos com eles.
num_layers
Este é o número de camadas ocultas da rede neural.
No hiperparâmetro anterior, hidden_size, determinamos o número de neurônios em cada camada oculta, agora vamos determinar quantas dessas camadas teremos.
Assim como o número de unidades, quanto mais camadas, maior a capacidade do modelo.
Mas tome cuidado, modelos de muitas camadas são mais fáceis de overfitar e demoram mais para treinar.
Por isso é necessário otimizar o número de camadas em vez de simplesmente jogar o maior número possível.
O intervalo padrão são números inteiros de 2 a 6.
Na prática vejo pouco ganho em usar mais de 3 camadas.
learning_rate
Este é o tamanho do passo que o algoritmo de otimização vai dar para atualizar os pesos da rede neural.
É um dos hiperparâmetros mais importantes e tem um grande impacto no desempenho do modelo.
Um valor muito alto pode fazer com que o modelo nunca estabilize, enquanto um valor muito baixo pode fazer com que o modelo demore muito para convergir.
O intervalo padrão é uma distribuição log uniforme entre 0.0001 e 0.1.
scaler_type
Este é o tipo de transformação que será aplicada nos dados antes de treinar o modelo.
Deixar os dados na mesma escala remodela a superfície de erro e permite que o modelo aprenda mais rápido e chegue a um resultado melhor.
A busca pode escolher entre None, standard e robust.
standard é a transformação mais comum que subtrai a média e divide pelo desvio padrão.
robust é uma transformação mais robusta que usa a mediana e o desvio absoluto da mediana
max_steps
Este é o número máximo de iterações que o algoritmo de otimização vai fazer para atualizar os pesos da rede neural.
Geralmente dar mais passos com uma learning_rate baixa te dá resultados mais estáveis, mas também leva mais tempo para treinar.
Os valores padrão são 500 e 1000.
batch_size
Este é o número de séries temporais diferentes que o algoritmo de otimização vai usar para calcular o gradiente para atualizar os pesos da rede neural em cada passo.
No nosso exemplo temos duas séries temporais, mas em casos com centenas ou milhares de séries, esse número faz diferença.
O intervalo padrão é para este hiperparâmetro é uma escolha entre 128, 256, 512 e 1024.
Mais uma vez, múltiplos de 2 porque as GPUs são mais eficientes com esses números.
windows_batch_size
Para cada série temporal original, a biblioteca criará várias séries menores baseadas no tamanho do horizonte e do número de observações que serão usadas como features.
O windows_batch_size é o número de janelas de dados que o algoritmo de otimização vai usar dentro de cada passo de atualização dos pesos da rede neural.
Parece confuso, mas vamos ver um exemplo.
Vamos juntar a learning_rate, max_steps, batch_size e windows_batch_size para entender melhor.
Com o batch_size decidimos quantas séries temporais originais vamos usar para calcular o gradiente para o passo atual.
Dentro desse lote de séries, vamos usar o windows_batch_size para determinar quantas subséries derivadas das séries originais estarão em cada lote de amostras.
Calculamos o gradiente sobre essas subséries, que nos dá a direção que o modelo deve seguir para ajustar os pesos da rede neural para minimizar a função de erro (o negativo do gradiente).
O número total de amostras em cada lote será batch_size * windows_batch_size.
Quanto mais amostras, mais preciso é o gradiente. Mas como outros parâmetros, nem sempre maior é melhor.
Vamos multiplicar esse negativo do gradiente pela learning_rate para ajustar o tamanho do passo que o algoritmo de otimização vai dar naquela direção.
E isso vai acontecer por um número máximo de vezes definido pelo max_steps.
Resumindo, o modelo será treinado sobre séries derivadas das séries originais em vez de usar cada série original diretamente.
Treinamento da Rede Neural
from neuralforecast import NeuralForecast
from neuralforecast.auto import AutoMLP
models = [AutoMLP(h=h,
num_samples=30,
loss=WMAPE())]
Primeiro criamos o objeto AutoMLP dentro de uma lista.
A lista é necessária porque você pode treinar vários modelos diferentes sobre os mesmos dados e comparar os resultados.
Como este é um tutorial sobre o AutoMLP, vamos usar apenas este modelo.
O argumento h é o horizonte de previsão, ou seja, quantos passos no futuro queremos prever, já definido anteriormente.
O argumento num_samples é o número de combinações de hiperparâmetros que o algoritmo de otimização vai testar.
Por padrão esta é uma busca aleatória.
Por experiência, 30 passos já vão te dar uma boa combinação de hiperparâmetros.
O argumento loss é a função de erro que o algoritmo de otimização vai tentar minimizar.
Neste caso criei uma função personalizada para calcular o WMAPE. No fim do artigo eu compartilho o código.
Se possível, otimizar diretamente a função de erro primária que você usará para avaliar o modelo é melhor.
model = NeuralForecast(models=models, freq='D')
model.fit(train)
Nesta parte criamos o objeto NeuralForecast, passamos a lista de modelos que queremos treinar e
o argumento freq que é a frequência de nossos dados.
Neste caso, como estamos trabalhando com dados diários, a frequência é D.
Depois chamamos o método fit passando o DataFrame de treino.
p = model.predict().reset_index()
p = p.merge(valid[['ds','unique_id', 'y']], on=['ds', 'unique_id'], how='left')
print("WMAPE:", wmape(p['y'], p['AutoMLP']))
Por fim, chamamos o método predict usando o modelo treinado para fazer as previsões.
Não temos variáveis externas neste caso, então o método predict não recebe argumentos.
Para facilitar a comparação com os dados de validação, fiz o merge da coluna y do DataFrame de validação com o DataFrame de previsões.
Estas são as 3 primeiras linhas do DataFrame p:
| unique_id | ds | AutoMLP | y |
|---|---|---|---|
| MEATS | 2017-01-01 00:00:00 | 158.957 | 0 |
| PERSONAL CARE | 2017-01-01 00:00:00 | 149.466 | 0 |
| PERSONAL CARE | 2017-01-02 00:00:00 | 100.162 | 81 |
As previsões estão na coluna AutoMLP e os valores reais estão na coluna y.
Imprimimos o WMAPE, que ficou em 21,99% quando rodei o código.
fig, ax = plt.subplots(2, 1, figsize = (1280/96, 720/96))
fig.tight_layout(pad=7.0)
for ax_i, unique_id in enumerate(['MEATS', 'PERSONAL CARE']):
plot_df = pd.concat([train.loc[train['unique_id'] == unique_id].tail(30),
p.loc[p['unique_id'] == unique_id]]).set_index('ds') # Concatenate the train and forecast dataframes
plot_df[['y', 'AutoMLP']].plot(ax=ax[ax_i], linewidth=2, title=unique_id)
ax[ax_i].grid()
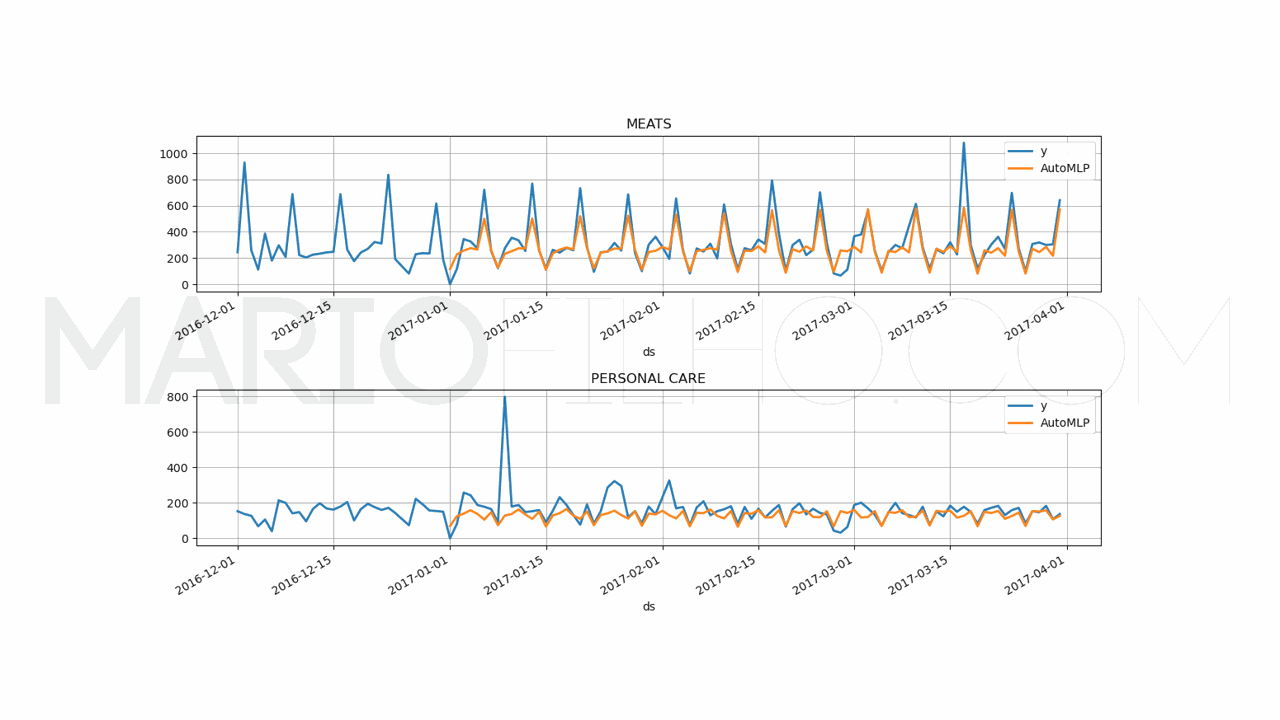
Por fim, plotamos os gráficos das previsões e dos valores reais para fazer uma comparação visual.
Na prática, nunca confie apenas nas métricas ou em gráficos individuais para avaliar o modelo!
Use métricas que te ofereçam perspectivas diferentes sobre os erros do modelo e avalie os gráficos em conjunto.
Podemos ver a melhor combinacão de hiperparâmetros com o método get_best_result sobre o atributo results do modelo.
best_config = models[0].results.get_best_result().metrics['config']
print(best_config)
{'h': 90,
'hidden_size': 512,
'num_layers': 5,
'learning_rate': 0.0017136606738724675,
'scaler_type': None,
'max_steps': 1000,
'batch_size': 256,
'windows_batch_size': 128,
'loss': WMAPE(),
'check_val_every_n_epoch': 100,
'random_seed': 10,
'input_size': 450,
'step_size': 1}
Vamos salvar esses hiperparâmetros na variável best_config para usar com as variáveis externas.
Também podemos ver os resultados de todas as combinações de hiperparâmetros com o método get_dataframe sobre o mesmo atributo.
results_df = models[0].results.get_dataframe().sort_values('loss')
results_df
| loss | config/num_layers | config/learning_rate | config/hidden_size |
|---|---|---|---|
| 0.236499 | 5 | 0.00171366 | 512 |
| 0.242066 | 5 | 0.000578393 | 1024 |
| 0.257967 | 4 | 0.00131074 | 1024 |
| 0.273158 | 5 | 0.0174233 | 1024 |
| 0.27565 | 2 | 0.000146954 | 512 |
Limitei as colunas para caber aqui, mas ele retorna o WMAPE e todos os valores de hiperparâmetros usados para treinar o modelo em cada passo da busca automática.
RuntimeError Por Falta de Dados
Em algumas tentativas de treinar o modelo com outras quantidades de dados, recebi o erro RuntimeError: maximum size for tensor at dimension 2 is 390 but size is 450.
Isso aconteceu porque eu não tinha dados suficientes para algumas combinações de hiperparâmetros.
Por exemplo, eu tentei usar dados de apenas um ano e ele queria fazer janelas de input_size com 450 dias.
Caso você veja esse erro, essa deve ser a razão. Tente usar mais dados, diminuir o input_size ou aumente o num_samples no AutoMLP e ignore as combinações de hiperparâmetros que não retornarem resultados.
Como Adicionar Variáveis Externas à Rede Neural
Na maioria dos casos de previsão de séries temporais, você terá variáveis externas relevantes que podem ser usadas para melhorar a previsão.
É muito simples adicionar essas variáveis externas ao modelo de redes neurais.
Para economizar tempo, vamos usar os mesmos hiperparâmetros, mas vamos treinar um modelo que também leve em conta a variável onpromotion e as variáveis para o dia da semana.
from neuralforecast import NeuralForecast
from neuralforecast.models import MLP
models = [MLP(futr_exog_list=['onpromotion', 'weekday_0',
'weekday_1', 'weekday_2', 'weekday_3', 'weekday_4', 'weekday_5',
'weekday_6'],
**best_config)]
model = NeuralForecast(models=models, freq='D')
model.fit(train)
p = model.predict(futr_df=valid).reset_index()
p = p.merge(valid[['ds','unique_id', 'y']], on=['ds', 'unique_id'], how='left')
print(wmape(p['y'], p['MLP']))
fig, ax = plt.subplots(2, 1, figsize = (1280/96, 720/96))
fig.tight_layout(pad=7.0)
for ax_i, unique_id in enumerate(['MEATS', 'PERSONAL CARE']):
plot_df = pd.concat([train.loc[train['unique_id'] == unique_id].tail(30),
p.loc[p['unique_id'] == unique_id]]).set_index('ds') # Concatenate the train and forecast dataframes
plot_df[['y', 'MLP']].plot(ax=ax[ax_i], linewidth=2, title=unique_id)
ax[ax_i].grid()
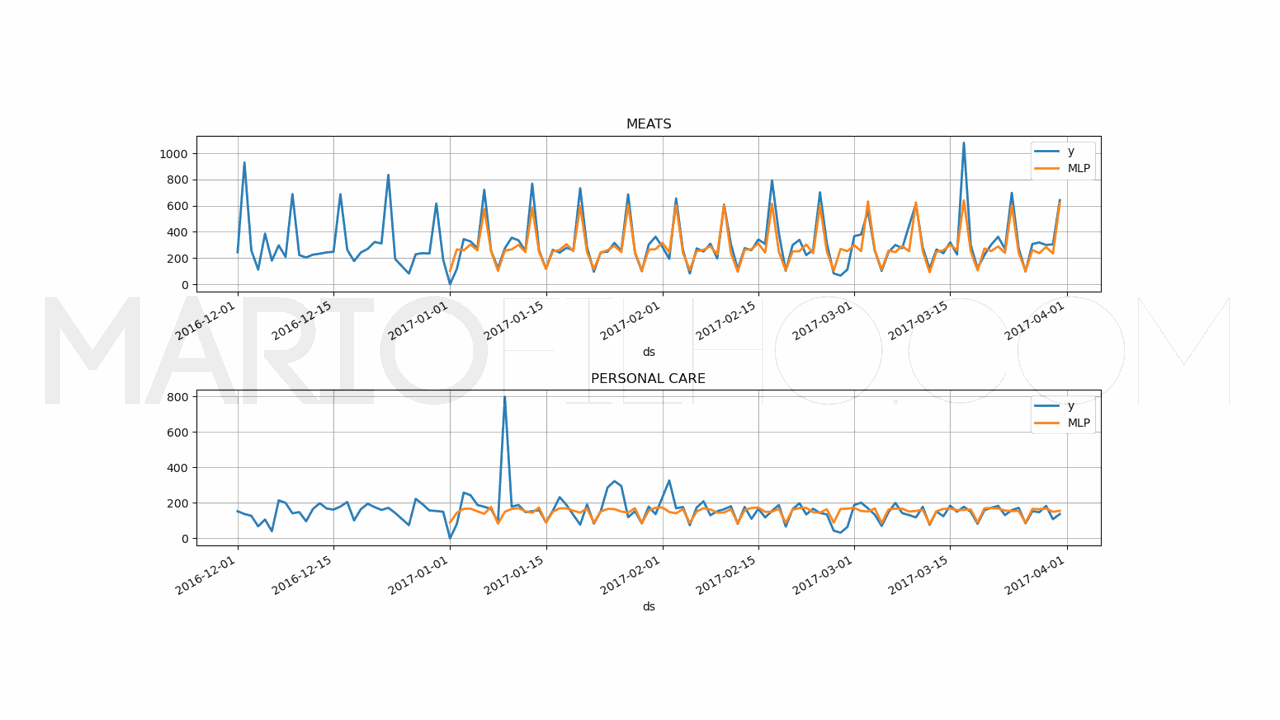
Existem poucas alterações no código acima:
- Vamos usar o objeto
MLPem vez doAutoMLP, já que não precisamos mais fazer a busca automática. - Adicionei a lista
futr_exog_listcom os nomes das variáveis externas que eu quero usar no modelo. Caso você queira adicionar variáveis externas estáticas (por exemplo, o código do produto), você pode usar o argumentostat_exog_list. - Usei a notação das ** para passar os valores do
best_configcomo argumentos nomeados para os hiperparâmetros do modelo. - No método
predict, precisamos passar um dataframe com as variáveis externas para cada passo futuro que queremos prever (cada dia). Neste caso precisamos saber em quais dias o produto estará em promoção além, é claro, do dia da semana.
Usando as variáveis externas junto com a própria série temporal, atingimos um WMAPE de 19,20%.
Ou seja, as variáveis externas ajudaram o modelo a capturar melhor os padrões para prever os valores futuros.
Baseline Simples Com Sazonalidade
Para saber se vale a pena colocar um modelo mais complexo em produção, é importante ter uma baseline simples para comparar.
Ela pode ser a solução atual usada em sua empresa ou uma solução simples como a média dos valores passados no mesmo período.
Neste caso, vou usar o objeto SeasonalNaive da biblioteca statsforecast que faz a previsão baseado neste método.
from statsforecast import StatsForecast
from statsforecast.models import SeasonalNaive
model = StatsForecast(models=[SeasonalNaive(season_length=7)], freq='D', n_jobs=-1)
model.fit(train)
forecast_df = model.predict(h=h, level=[90])
forecast_df = forecast_df.reset_index().merge(valid, on=['ds', 'unique_id'], how='left')
wmape_ = wmape(forecast_df['y'], forecast_df['SeasonalNaive'])
print(f'WMAPE: {wmape_:.2%}')
fig, ax = plt.subplots(2, 1, figsize = (1280/96, 720/96))
fig.tight_layout(pad=7.0)
for ax_i, unique_id in enumerate(['MEATS', 'PERSONAL CARE']):
plot_df = pd.concat([train.loc[train['unique_id'] == unique_id].tail(30),
forecast_df.loc[p['unique_id'] == unique_id]]).set_index('ds') # Concatenate the train and forecast dataframes
plot_df[['y', 'SeasonalNaive']].plot(ax=ax[ax_i], linewidth=2, title=unique_id)
ax[ax_i].grid()
Visite este artigo para entender melhor o código acima e como usar baselines e métodos estatísticos para prever séries temporais.
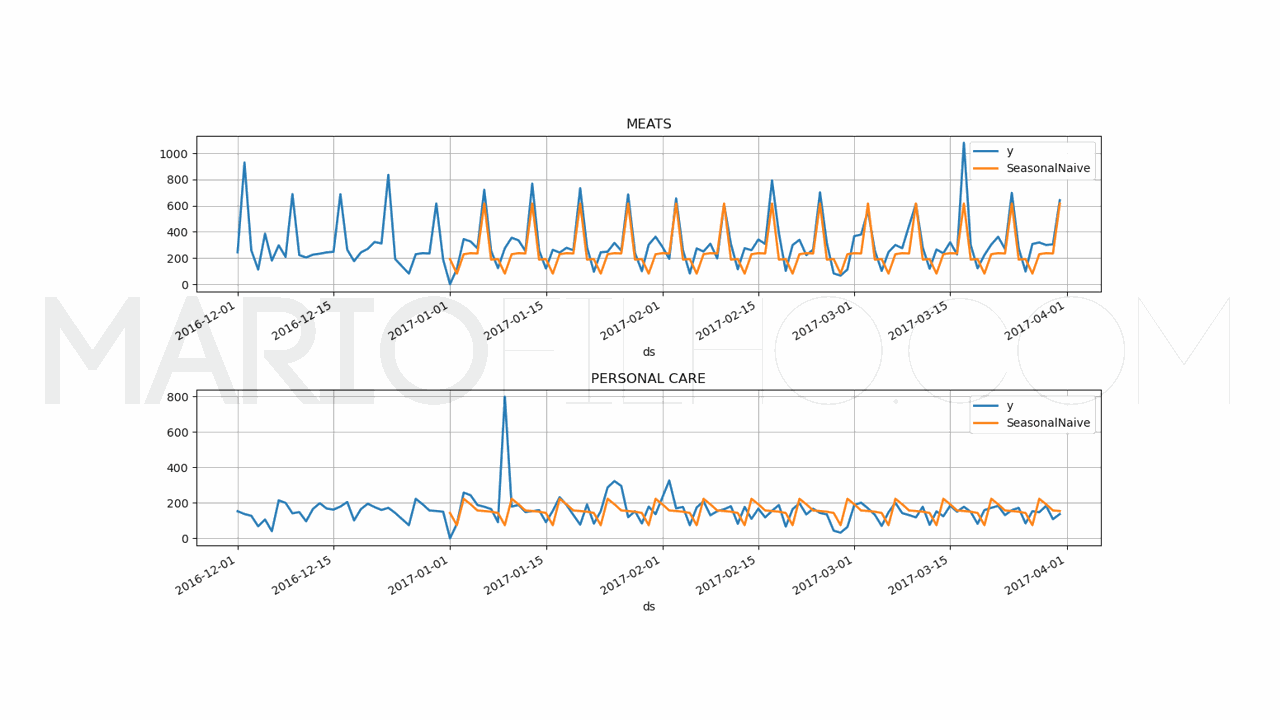
Esta baseline retornou um WMAPE de 31,53% que não bate o modelo de redes neurais com ou sem variáveis externas.
Ou seja, nosso modelo de redes neurais está aprendendo padrões úteis além dos básicos de sazonalidade e usando-os para fazer previsões melhores.
Loss Function Personalizada com PyTorch (WMAPE)
Como prometido, esta é a função personalizada que criei, já que o PyTorch não tem uma loss function para o WMAPE.
import torch
from typing import Union
class WMAPE(torch.nn.Module):
def __init__(self):
super(WMAPE, self).__init__()
self.outputsize_multiplier = 1
self.output_names = [""]
self.is_distribution_output = False
def domain_map(self, y_hat: torch.Tensor):
return y_hat.squeeze(-1)
def __call__(
self,
y: torch.Tensor,
y_hat: torch.Tensor,
mask: Union[torch.Tensor, None] = None,
):
if mask is None:
mask = torch.ones_like(y_hat)
num = mask * (y - y_hat).abs()
den = mask * y.abs()
return num.sum() / den.sum()
