Índice
- O Que São Redes Neurais Convolucionais?
- Redes Convolucionais Temporais
- Como Instalar a NeuralForecast Com e Sem Suporte a GPU
- Como Preparar a Série Temporal Para A Rede Neural Convolucional
- Hiperparâmetros e Arquitetura da TCN
- Treinamento da Rede Neural
- Como Adicionar Variáveis Externas à Rede Neural Convolucional
- Baseline Simples Com Sazonalidade
- Função Objetivo WMAPE no PyTorch
O Que São Redes Neurais Convolucionais?
Redes Neurais Convolucionais (CNN) são redes neurais pensadas para processar dados com alguma estrutura espacial.
Os exemplos mais famosos estão na área de visão computacional, onde as imagens são representadas como matrizes e as CNNs são usadas para extrair características relevantes para prever um alvo.
As convoluções são como filtros que são aplicados sobre os dados.
A diferença entre aplicar uma rede convolucional ou um filtro pré-definido é que a rede aprende os filtros mais relevantes para os dados apresentados.
Uma média móvel pode ser vista como um filtro convolucional: ela multiplica cada valor da série por um peso e soma os resultados.
Redes Convolucionais Temporais
A WaveNet foi um dos primeiros sucessos de redes neurais convolucionais aplicadas a séries temporais.
Ela ficou conhecida, de forma mais geral, como Rede Convolucional Temporal.
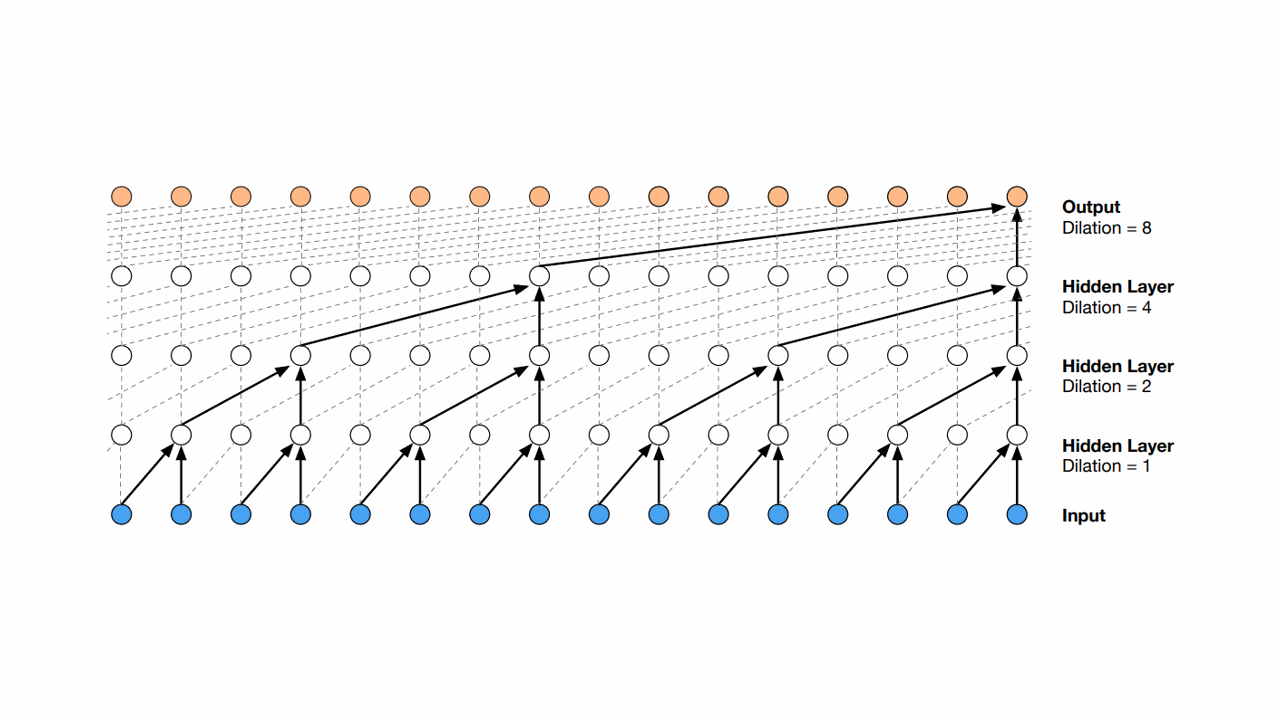 Fonte: WaveNet: A Generative Model for Raw Audio
Fonte: WaveNet: A Generative Model for Raw Audio
O ingrediente principal que a torna diferente de outras redes convolucionais é que ela usa “convoluções causais e dilatadas”.
As convoluções causais forçam o modelo a aprender a dependência entre os passos sem violar a ordem natural do tempo.
Isso é diferente de outras redes convolucionais que consideram todos os dados disponíveis numa sequência para fazer a modelagem.
A técnica de dilatação faz com que ela considere uma porção cada vez maior de passos da série temporal conforme avança nas camadas mais profundas.
Em geral, como você pode ver na imagem, o fator de dilatação é dobrado a cada camada.
A unidade 2 na primeira camada oculta processa as informações das observações 1 e 2.
Já a unidade 4 da segunda camada oculta processa as observações 1, 2, 3 e 4 através do processamento das unidades ocultas 2 e 4 da primeira camada oculta.
E assim vai.
Isso resulta em um crescimento exponencial do campo receptivo conforme a rede vai avançando às camadas mais profundas.
Essas redes são geralmente mais rápidas de treinar do que as redes recorrentes.
Com a biblioteca NeuralForecast ficou muito fácil treinar essa rede rapidamente em seus dados e é isso que você vai aprender agora.
Como Instalar a NeuralForecast Com e Sem Suporte a GPU
Por usar métodos de redes neurais, se você tiver uma GPU, é importante ter o CUDA instalado para que os modelos rodem mais rápido.
Para verificar se você tem uma GPU instalada e configurada corretamente com PyTorch (backend da biblioteca), execute o código abaixo:
import torch
print(torch.cuda.is_available())
Esta função retorna True se você tem uma GPU instalada e configurada corretamente, e False caso contrário.
Caso você tenha uma GPU, mas não tenha o PyTorch instalado com suporte a ela, veja no site oficial como instalar a versão correta.
Recomendo que você instale o PyTorch primeiro!
O comando que usei para instalar o PyTorch com suporte a GPU foi:
conda install pytorch pytorch-cuda=11.7 -c pytorch -c nvidia
Se você não tem uma GPU, não se preocupe, a biblioteca funciona normalmente, só não fica tão rápida.
Instalar essa biblioteca é muito simples, basta executar o comando abaixo:
pip install neuralforecast
ou se você usa o Anaconda:
conda install -c conda-forge neuralforecast
Como Preparar a Série Temporal Para A Rede Neural Convolucional
Vamos usar dados reais de vendas da rede de lojas Favorita, do Equador.
Temos dados de vendas de 2013 a 2017 para diversas lojas e categorias de produtos.
Nossos dados de treino cobrirão os anos 2013 a 2016 e os dados de validação serão os 3 primeiros meses de 2017.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
def wmape(y_true, y_pred):
return np.abs(y_true - y_pred).sum() / np.abs(y_true).sum()
Para medir o desempenho do modelo, vamos usar a métrica WMAPE (Weighted Mean Absolute Percentage Error).
Ela é uma adaptação do erro percentual que resolve o problema de dividir por zero.
No nosso caso, vamos considerar que o peso de cada observação é o valor absoluto dela, simplificando a fórmula.
data = pd.read_csv('train.csv', index_col='id', parse_dates=['date'])
data2 = data.loc[(data['store_nbr'] == 1) & (data['family'].isin(['MEATS', 'PERSONAL CARE'])), ['date', 'family', 'sales', 'onpromotion']]
Para simplificar, vamos usar apenas os dados de uma loja e duas categorias de produto.
As colunas são:
date: data do registrofamily: categoria do produtosales: número de vendasonpromotion: a quantidade de produtos daquela categoria que estavam em promoção naquele dia
weekday = pd.get_dummies(data2['date'].dt.weekday)
weekday.columns = ['weekday_' + str(i) for i in range(weekday.shape[1])]
data2 = pd.concat([data2, weekday], axis=1)
Além das vendas e indicador de promoções, vamos criar variáveis adicionais do dia da semana.
O dia da semana pode ser tratado como uma variável ordinal ou categórica, mas aqui vou usar a abordagem categórica que é mais comum.
Em geral, usar informações adicionais que sejam relevantes para o problema pode melhorar o desempenho do modelo.
Variáveis específicas da estrutura temporal, como dias da semana, meses e dias do mês são importantes para capturar padrões sazonais.
Existe uma infinidade de outras informações que poderíamos adicionar, como a temperatura, chuva, feriados, etc.
Nem sempre essas informações vão melhorar o modelo, e podem até piorar o desempenho, então sempre verifique se elas melhoram o erro nos dados de validação.
data2 = data2.rename(columns={'date': 'ds', 'sales': 'y', 'family': 'unique_id'})
A biblioteca neuralforecast espera que as colunas sejam nomeadas dessa forma:
ds: data do registroy: variável alvo (número de vendas)unique_id: identificador único da série temporal (categoria do produto)
O unique_id pode ser qualquer identificador que separe suas séries temporais.
Se quiséssemos modelar a previsão de vendas de todas as lojas, poderíamos usar o store_nbr junto com a family como identificadores.
train = data2.loc[data2['ds'] < '2017-01-01']
valid = data2.loc[(data2['ds'] >= '2017-01-01') & (data2['ds'] < '2017-04-01')]
h = valid['ds'].nunique()
Este é o formato final da tabela:
| ds | unique_id | y | onpromotion | weekday_0 | weekday_1 | weekday_2 | weekday_3 | weekday_4 | weekday_5 | weekday_6 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2013-01-01 00:00:00 | MEATS | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2013-01-01 00:00:00 | PERSONAL CARE | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2013-01-02 00:00:00 | MEATS | 369.101 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
Separamos os dados em treino e validação com uma divisão temporal simples entre passado e futuro.
A variável h é o horizonte, o número de períodos que queremos prever no futuro.
Neste caso, é o número de datas únicas na validação (90).
Vamos para a modelagem.
Hiperparâmetros e Arquitetura da TCN
A implementação da TCN nesta biblioteca segue o padrão encoder-decoder.
A ideia é usar uma TCN para aprender uma representação numérica otimizada das observações passadas (encoder) e depois passar essa representação para uma rede neural comum (decoder) que vai gerar as previsões.
Existem vários hiperparâmetros que podem ser ajustados, mas a biblioteca nos dá uma classe que fará a busca automática aleatória pela melhor combinação com base no erro de validação.
Ainda assim é importante entender quais são eles e o intervalo de valores padrão que a biblioteca usa para otimizá-los.
Recomendo que você faça a busca usando o intervalo padrão, principalmente se você ainda não tem muita experiência com redes neurais.
Os números mostrados aqui como opções padrão não são necessariamente os únicos possíveis, mas apenas intervalos escolhidos pelo criador da biblioteca como sensatos para otimizar.
kernel_size
Este é o tamanho de cada filtro usado nas camadas de convolução da TCN.
Um filtro é simplesmente um vetor de pesos que é aplicado deslizando-o sobre a série temporal para gerar uma nova sequência de valores.
Podemos pensar nessa nova sequência como uma transformação da série temporal.
Se temos uma série temporal com 10 observações e um filtro com tamanho 2, primeiro multiplicamos seus dois pesos pelos dois primeiros valores da série temporal e somamos o resultado.
Isso nos dá o valor do primeiro elemento da sequência transformada.
No segundo passo, multiplicamos os dois pesos pelos valor 2 e 3 da série temporal e somamos o resultado para obter o segundo elemento da sequência transformada.
E assim vai até o último.
Aplicamos vários filtros diferentes para gerar várias sequências transformadas.
A ideia é que essas transformações representem melhor os padrões que precisamos para prever as próximas observações.
Este hiperparâmetro não é otimizado durante a busca automática e recebe o valor padrão de 2, igual ao diagrama original da TCN.
dilations
Este é o valor do intervalo de dilatação dos filtros, quantas unidades de tempo eles devem pular ao aplicar a transformação.
Também são valores fixos, múltiplos de 2, conforme o diagrama acima.
input_size_multiplier
O primeiro valor otimizado na busca automática.
Ele define o número de observações que serão usadas como entrada para a TCN.
Os valores possíveis são -1, 4, 16 e 64.
Mas preste atenção, esse valor é multiplicado pelo horizonte!
Ou seja, um valor igual a 4 significa que serão usadas 4 vezes o horizonte como entrada (4 * 90 = 360 dias no nosso exemplo).
Caso o valor seja -1, o objeto passará todas as observações passadas como entrada.
encoder_hidden_size
Este é o tamanho da representação (oculta) otimizada que será retornada pela TCN, que também é o número de filtros aplicados.
O número de unidades desta representação afeta diretamente a capacidade da rede de aprender padrões complexos.
Quanto maior, mais complexos os padrões que ela pode aprender, mas também maior a chance de overfitting.
Este hiperparâmetro é otimizado durante a busca automática, seus valores possíveis são 50, 100, 200 ou 300.
context_size
Antes de passar os valores de saída da TCN para o decoder, eles são transformados novamente para representar o contexto geral das informações da série temporal.
Podemos pensar nisso como um resumo das informações mais importantes que precisamos para fazer as previsões das próximas observações.
Ele é um vetor de tamanho definido pelo context_size.
Os valores possíveis para este hiperparâmetro são 5, 10 e 50.
decoder_hidden_size
Este é o número de unidades nas camadas ocultas da rede neural MLP que será usada como decoder.
Ela tem duas camadas ocultas por padrão, e este é o número de unidades em cada uma delas, não o total entre elas.
Dois valores são testados durante a busca: 64 e 128.
learning_rate
Um dos hiperparâmetros mais impactantes, ela define quanto cada passo da otimização irá modificar os pesos da rede.
Quanto menor a learning_rate, mais lenta a otimização, mas também mais estável.
Durante a busca o valor é escolhido através da amostragem de uma distribuição log uniforme e pode variar entre 0.0001 e 0.1.
max_steps
O número máximo de vezes que a rede neural vai atualizar os pesos durante a otimização.
Ele é intimamente ligado à learning_rate e tende a ser maior quanto menor for o valor dela.
Dois valores são testados: 500 e 1000.
batch_size
O número de exemplos que serão usados para calcular o gradiente para atualizar os pesos da rede neural em cada passo da otimização.
Cada exemplo é uma série derivada da série original, com um tamanho definido pelo input_size_multiplier.
A busca testa dois valores: 16 e 32.
Treinamento da Rede Neural
Com os dados prontos, fazer a busca automática é bem simples.
from neuralforecast import NeuralForecast
from neuralforecast.auto import AutoTCN
models = [AutoTCN(h=h,
num_samples=30,
loss=WMAPE())]
model = NeuralForecast(models=models, freq='D')
model.fit(train)
Após importarmos os objetos AutoTCN e NeuralForecast, criamos uma lista com um único objeto AutoTCN e passamos para o objeto NeuralForecast.
A biblioteca permite treinar vários modelos diferentes num mesmo objeto, mas por ser um tutorial, vamos usar apenas o objeto da TCN.
O objeto AutoTCN recebe os seguintes argumentos:
h: o horizonte de previsão (quantos passos no futuro queremos prever)num_samples: o número de combinações de hiperparâmetros que serão testadas durante a busca automática
Por padrão, a busca é aleatória, mas também poderíamos usar otimização bayesiana.
Na prática, testar 30 combinações acha uma boa solução em um tempo razoável.
No objeto NeuralForecast passamos o argumento freq que define a frequência da série temporal. No nosso caso, é diária.
Agora, basta chamar o método fit e passar os dados de treino para iniciar o treinamento.
p = model.predict().reset_index()
p = p.merge(valid[['ds','unique_id', 'y']], on=['ds', 'unique_id'], how='left')
Com o modelo treinado, podemos fazer as previsões usando o método predict.
Juntei os dados de previsão com os de validação para facilitar a visualização e o cálculo do erro.
| unique_id | ds | AutoTCN | y |
|---|---|---|---|
| MEATS | 2017-01-01 00:00:00 | 159.179 | 0 |
| PERSONAL CARE | 2017-01-01 00:00:00 | 147.123 | 0 |
| PERSONAL CARE | 2017-01-02 00:00:00 | 82.5419 | 81 |
fig, ax = plt.subplots(2, 1, figsize = (1280/96, 720/96))
fig.tight_layout(pad=7.0)
for ax_i, unique_id in enumerate(['MEATS', 'PERSONAL CARE']):
plot_df = pd.concat([train.loc[train['unique_id'] == unique_id].tail(30),
p.loc[p['unique_id'] == unique_id]]).set_index('ds') # Concatenate the train and forecast dataframes
plot_df[['y', 'AutoTCN']].plot(ax=ax[ax_i], linewidth=2, title=unique_id)
ax[ax_i].grid()
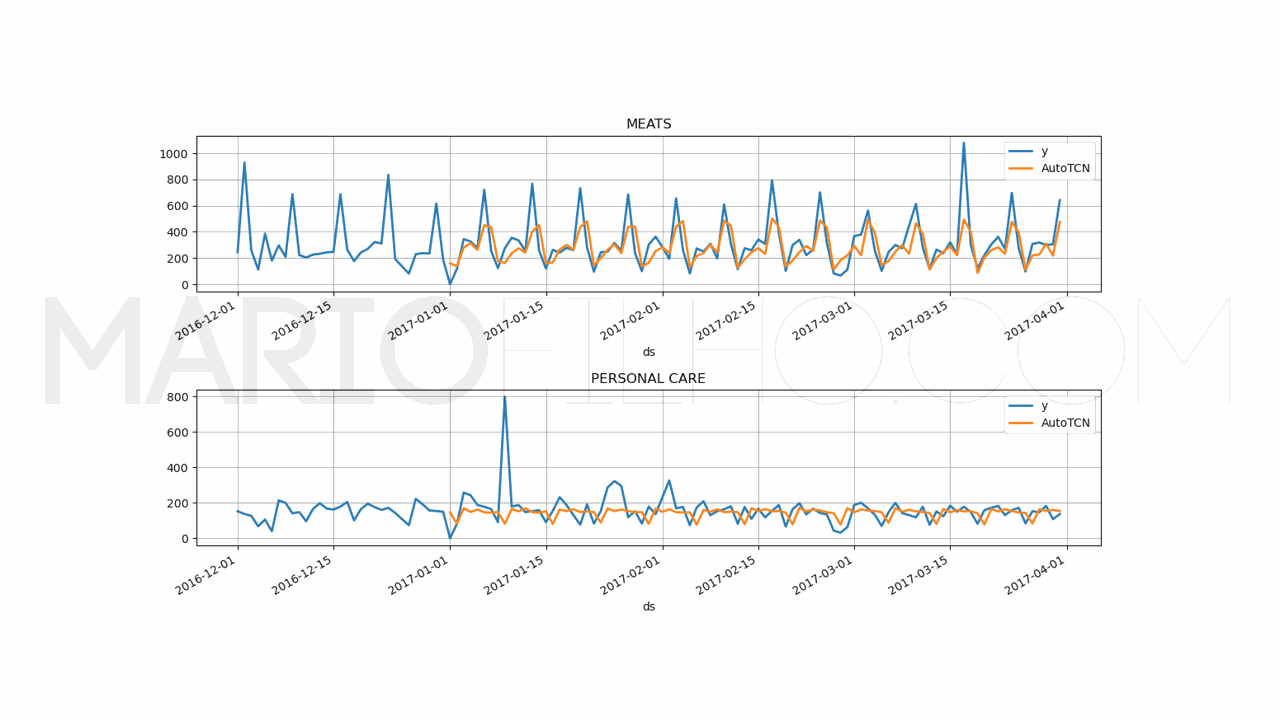
Por fim verificamos o WMAPE da melhor combinação sobre nossos dados de validação, que ficou em 31,53%.
print(wmape(p['y'], p['AutoTCN']))
Se você quiser ver todas as combinações testadas, basta usar o método get_dataframe.
results_df = models[0].results.get_dataframe().sort_values('loss')
results_df
Ele retorna um DataFrame com os valores usados em cada hiperparâmetro e o erro daquela combinação na validação interna da busca.
Isso é muito útil para entender quais hiperparâmetros estão influenciando mais o resultado e guiar seus próximos experimentos.
| loss | config/encoder_hidden_size | config/decoder_hidden_size | config/max_steps |
|---|---|---|---|
| 0.685285 | 200 | 64 | 500 |
| 0.695898 | 50 | 128 | 1000 |
| 0.69598 | 100 | 64 | 1000 |
| 0.697506 | 200 | 128 | 500 |
| 0.702176 | 100 | 64 | 1000 |
Além disso, usando o método get_best_result podemos ver qual foi a melhor combinação e usá-la para treinar modelos futuros.
best_config = models[0].results.get_best_result().metrics['config']
best_config
{'h': 90,
'encoder_hidden_size': 200,
'context_size': 10,
'decoder_hidden_size': 64,
'learning_rate': 0.0001565744688888989,
'max_steps': 500,
'batch_size': 16,
'loss': WMAPE(),
'check_val_every_n_epoch': 100,
'random_seed': 9,
'input_size': -90}
Vamos usar essa configuração para treinar um modelo usando variáveis externas além da própria série temporal e ver se conseguimos melhorar o resultado.
Como Adicionar Variáveis Externas à Rede Neural Convolucional
Este é o código completo para treinar a TCN usando variáveis externas e a melhor configuração encontrada pelo AutoTCN.
from neuralforecast import NeuralForecast
from neuralforecast.models import TCN
models = [TCN(futr_exog_list=['onpromotion', 'weekday_0',
'weekday_1', 'weekday_2', 'weekday_3', 'weekday_4', 'weekday_5',
'weekday_6'],
**best_config)]
model = NeuralForecast(models=models, freq='D')
model.fit(train)
p = model.predict(futr_df=valid).reset_index()
p = p.merge(valid[['ds','unique_id', 'y']], on=['ds', 'unique_id'], how='left')
fig, ax = plt.subplots(2, 1, figsize = (1280/96, 720/96))
fig.tight_layout(pad=7.0)
for ax_i, unique_id in enumerate(['MEATS', 'PERSONAL CARE']):
plot_df = pd.concat([train.loc[train['unique_id'] == unique_id].tail(30),
p.loc[p['unique_id'] == unique_id]]).set_index('ds') # Concatenate the train and forecast dataframes
plot_df[['y', 'TCN']].plot(ax=ax[ax_i], linewidth=2, title=unique_id)
ax[ax_i].grid()
print(wmape(p['y'], p['TCN']))
Precisamos fazer poucas modificações:
- Em vez de usar o objeto
AutoTCN, usamos o objetoTCNpara treinar o modelo. Esse objeto treina uma TCN sem fazer a busca de hiperparâmetros. - Passamos a lista com os nomes das variáveis externas que queremos usar como argumento
futr_exog_listdo objetoTCN. Caso você queira adicionar variáveis externas estáticas (por exemplo, o código do produto), você pode usar o argumentostat_exog_list. - Passamos o dicionário
best_configcomo argumentos nomeados do objetoTCN. Assim ele treinará a rede usando essa configuração. - No método
predict, passamos o DataFrame com os valores futuros para cada período que queremos prever. Por exemplo, se naquele dia planejamos ter uma promoção, passamos o valor 1 para a variávelonpromotione 0 caso contrário.
Este foi o resultado:
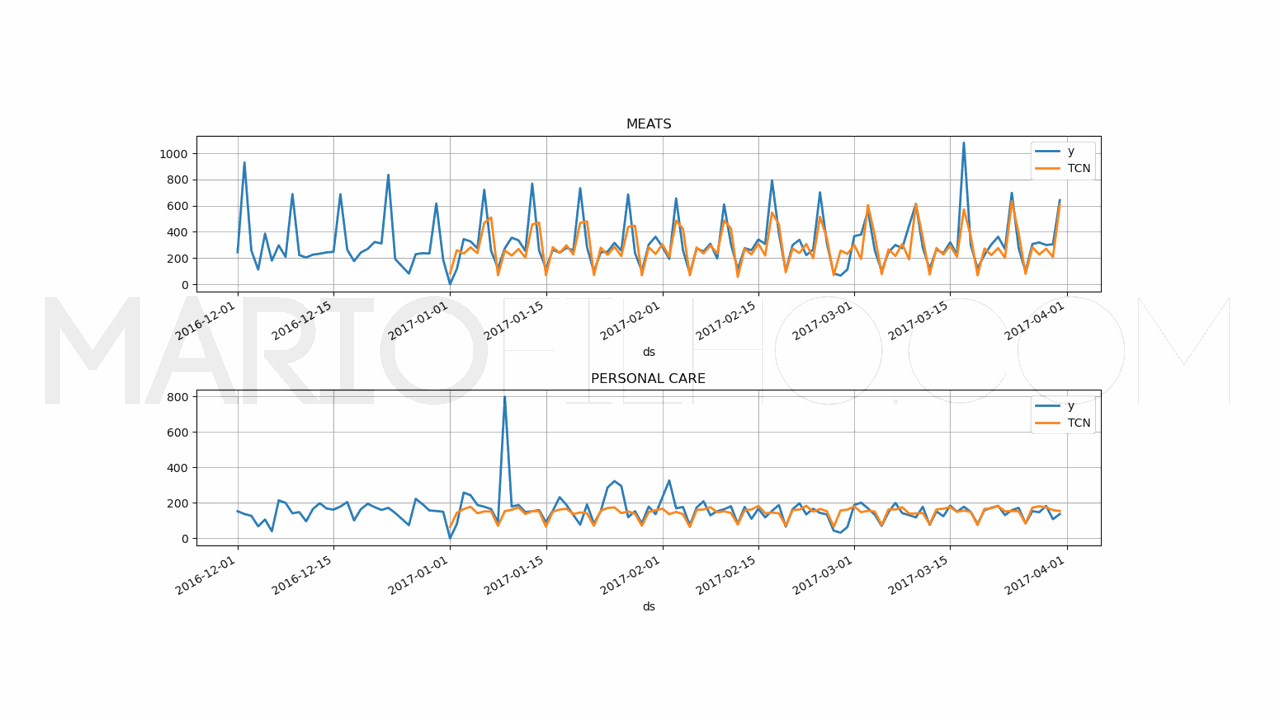
O WMAPE caiu para 25,91%.
Muito bom! Indicar o dia da semana e se haverá promoção naquele dia ajudou a melhorar o resultado.
Baseline Simples Com Sazonalidade
Para saber se vale a pena colocar um modelo mais complexo em produção, é importante ter uma baseline simples para comparar.
Ela pode ser a solução atual usada em sua empresa ou uma solução simples como a média dos valores passados no mesmo período.
Vamos usar a baseline de sazonalidade, que é uma técnica simples que usa a média dos valores passados no mesmo período do ano.
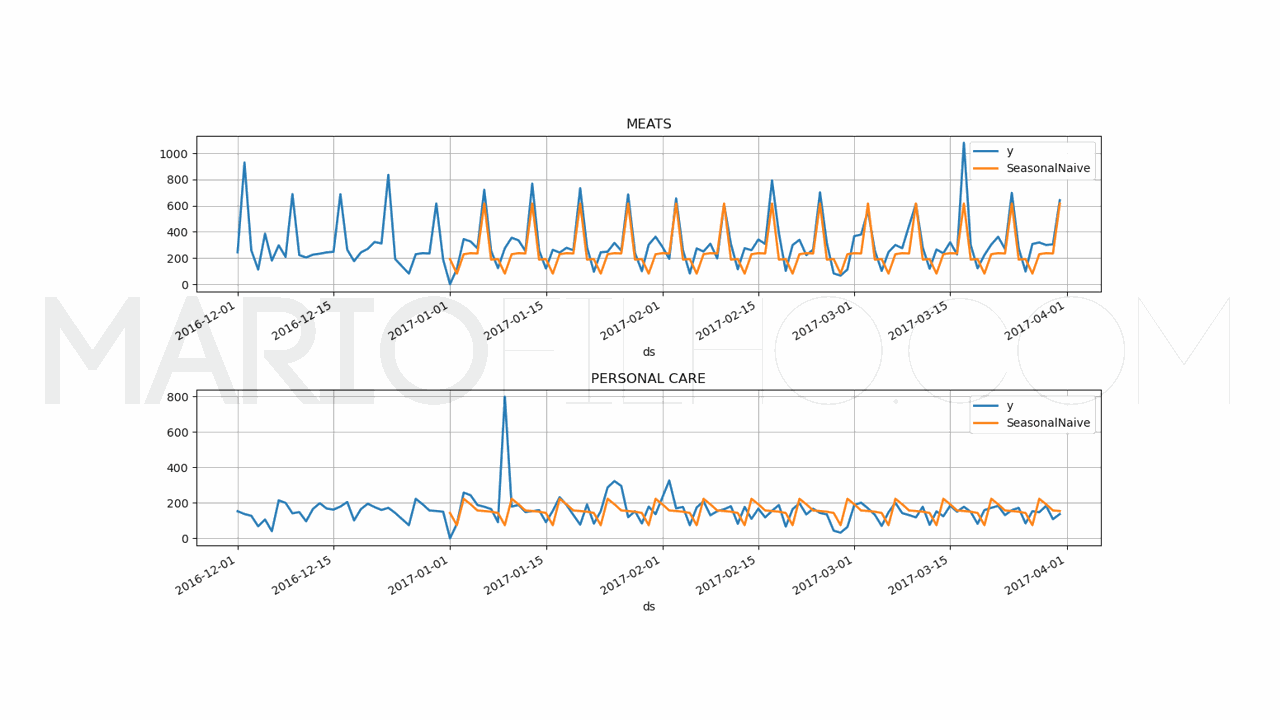
Esta baseline possui um WMAPE de 31,53%.
Neste caso, nosso modelo de TCN com variáveis externas é melhor que a baseline e temos mais confiança em colocá-lo em produção.
Visite este artigo para ver como calcular essa baseline.
Função Objetivo WMAPE no PyTorch
Veja aqui o código completo da implementação da função objetivo WMAPE no PyTorch.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.