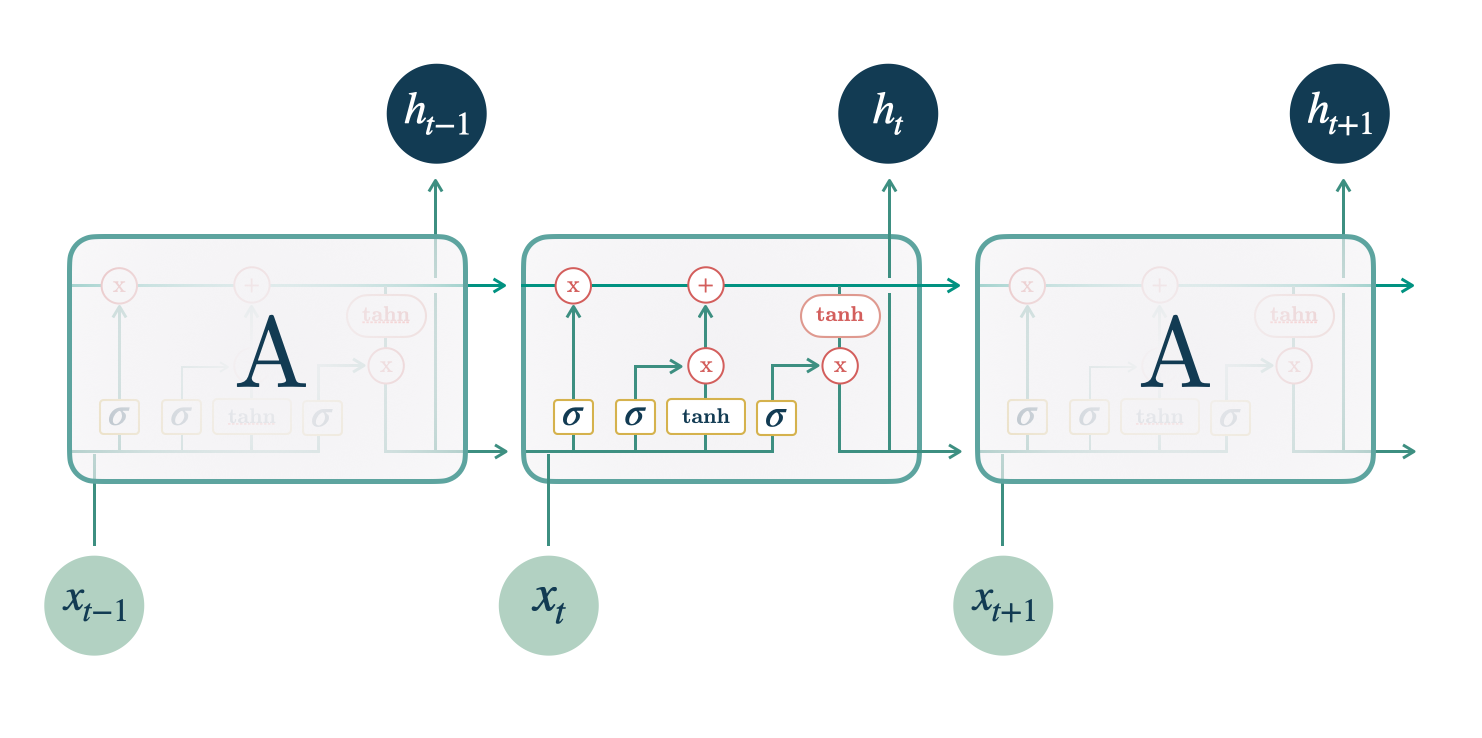
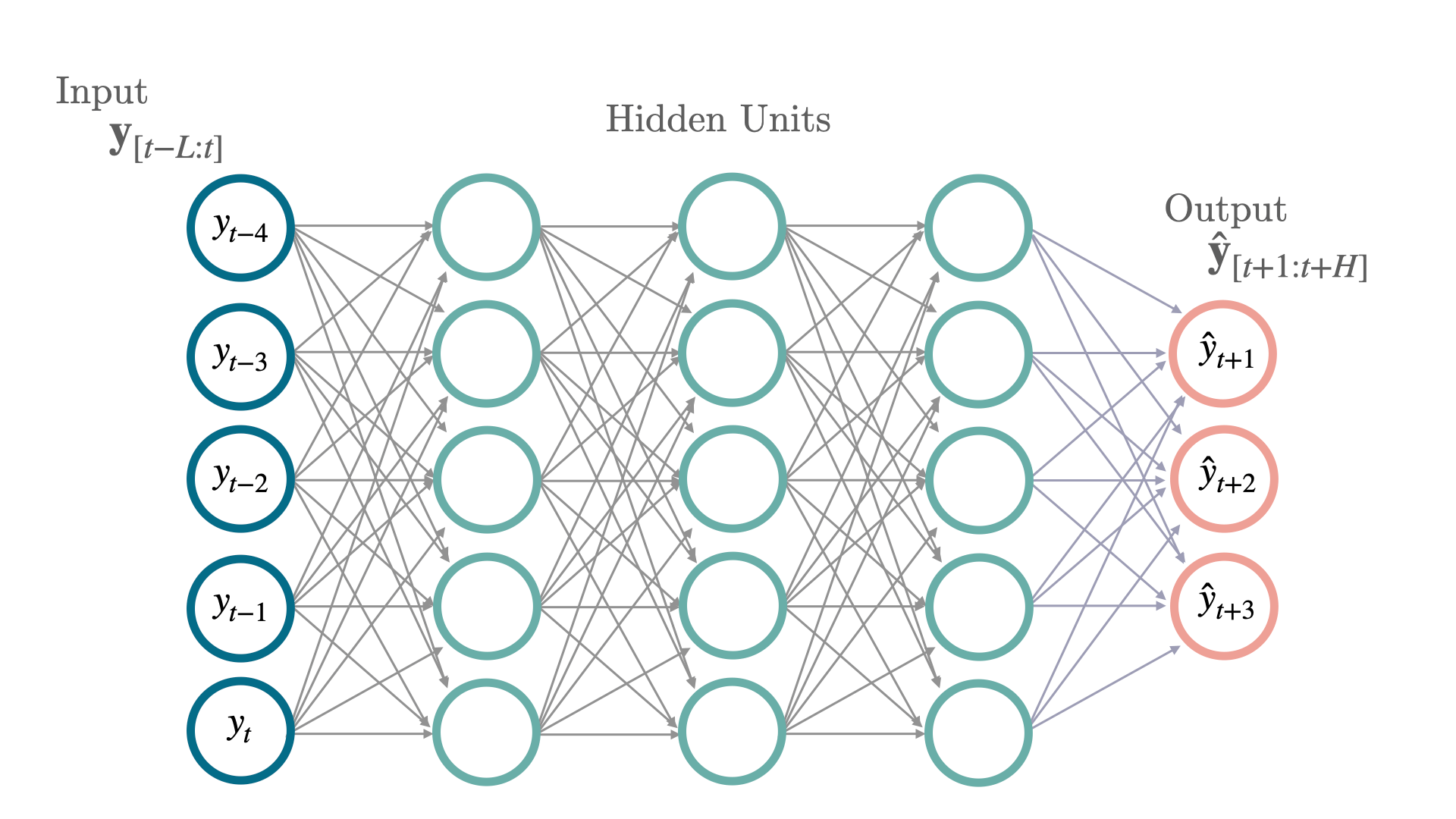
A modelagem de séries temporais com deep learning (redes neurais) é uma área em constante evolução. Falar de “redes neurais” pode se referir a vários tipos diferentes de técnicas como redes neurais convolucionais, redes neurais recorrentes, redes neurais tradicionais (MLP) e redes neurais com mecanismo de atenção (transformer). Por isso, primeiro vou te dar uma visão geral dessas técnicas, indicando artigos mais detalhados sobre cada uma e depois vou te mostrar como aplicar uma rede neural tradicional (MLP) para prever séries temporais....

Índice O Que é LSTM (Long Short-Term Memory)? Como Funciona a LSTM? Quando Usar a LSTM? Como Instalar a NeuralForecast Com e Sem Suporte a GPU Como Preparar os Dados Para a LSTM Modelagem Automática com AutoLSTM Arquitetura da LSTM Busca Automática por Hiperparâmetros input_size_multiplier encoder_hidden_size encoder_n_layers decoder_hidden_size learning_rate max_steps batch_size random_seed Código de Treinamento da LSTM em Python Análise dos Resultados da Busca Automática LSTM com Variáveis Adicionais Baseline Simples Com Sazonalidade Loss Function Personalizada com PyTorch (WMAPE) O Que é LSTM (Long Short-Term Memory)?...

De todos os tipos de previsão, prever o que ocorrerá no futuro com base em eventos passados pode ser uma das tarefas mais interessantes e desafiadoras. É aí que entra a previsão de séries temporais. Prever uma série temporal começa por supor que os padrões de comportamento observados no passado serão replicados no futuro. Uma das maneiras de fazer estas previsões é usando modelos estatísticos sobre séries univariadas, que é o que você vai aprender neste artigo usando Python....

Ao usar machine learning para prever séries temporais, você não pode simplesmente dividir seus dados entre treino e validação com um split aleatório. Se você fizer isso, seu modelo vai aprender a prever o passado com base no futuro e te dar uma estimativa altamente otimista (e errada) da performance em dados nunca vistos. Em praticamente todos os projetos reais de machine learning você terá uma dimensão temporal e jamais deve ignorá-la....

Índice O Que São Séries Temporais? Quais São Os Principais Tipos De Séries Temporais? Diferença Entre Série Temporal Univariada e Multivariada Diferença Entre Série Temporal Estacionária e Não Estacionária Diferença Entre Série Temporal Regular e Irregular Quais São Os Componentes De Uma Série Temporal? Decomposição Aditiva de Séries Temporais Tendência Em Séries Temporais Sazonalidade Em Séries Temporais Ciclo Em Séries Temporais Ruído Em Séries Temporais O Que É Lag Na Análise de Séries Temporais?...

Índice O Que é Mean Average Precision? Qual a Fórmula da Mean Average Precision? Como Interpretar a Mean Average Precision? Como Calcular a Mean Average Precision em Python? Qual a Diferença Entre Mean Average Precision e NDCG? Qual a Diferença Entre Mean Average Precision e Mean Reciprocal Rank? O Que é Mean Average Precision? Mean Average Precision (MAP) é uma métrica de avaliação em machine learning comumente usada para medir a performance de sistemas de recomendação e busca....

Índice O Que é NDCG? Como Interpretar o NDCG? Qual a Fórmula do NDCG? Como Calcular o NDCG em Python? Qual a Diferença Entre NDCG e Mean Average Precision? Qual a Diferença Entre NDCG e Mean Reciprocal Rank? O Que é NDCG? O NDCG é uma métrica de avaliação de desempenho que é especialmente útil para modelos de machine learning de ranking. Ela é muito usada em sistemas de busca e recomendação....

Índice O Que é Mean Reciprocal Rank? Qual a Fórmula do Mean Reciprocal Rank? Como Interpretar o Mean Reciprocal Rank? Como Calcular o Mean Reciprocal Rank em Python? Qual a Diferença Entre Mean Reciprocal Rank e NDCG? Qual a Diferença Entre Mean Reciprocal Rank e Mean Average Precision? O Que é Mean Reciprocal Rank? O Mean Reciprocal Rank (MRR) é uma métrica comumente utilizada para avaliar a qualidade de modelos de machine learning que retornam uma lista de resultados relevantes....

Índice O Que é Erro Absoluto Percentual Médio ou MAPE? Qual a Fórmula do MAPE? Como Interpretar o MAPE? Como Calcular o MAPE Usando Scikit-learn em Python? Como Calcular o MAPE em R? Qual a Diferença Entre MAPE e WMAPE? Qual a Diferença Entre MAPE e WAPE? Qual a Diferença Entre MAPE e SMAPE? Qual a Diferença Entre MAPE e RMSE? Qual a Diferença Entre MAPE e MAE? O Que é Erro Absoluto Percentual Médio ou MAPE?...

Índice O Que é Erro Médio Absoluto ou MAE? Qual a Fórmula do MAE? Como Interpretar o MAE? Como Calcular o MAE Usando Scikit-learn em Python? Como Calcular o MAE em R? Diferença Entre Erro Absoluto e Relativo Diferença Entre MAE e MSE Diferença Entre MAE e MAPE O MAE Pode Ser Usado Para Avaliar Modelos De Classificação? O Que é Erro Médio Absoluto ou MAE? O erro médio absoluto (MAE) é uma métrica utilizada para avaliar o desempenho de modelos de regressão em machine learning....