Você está tendo dificuldades para fazer seus modelos de regressão performarem bem?
Talvez você tenha tentado vários algoritmos, ajustado seus parâmetros e até coletado mais dados, mas as previsões do seu modelo ainda estão imprecisas.
Neste tutorial, vou apresentar a você o XGBoost, um poderoso algoritmo de machine learning que, além de vencer competições no Kaggle, é muito utilizado em produção por empresas como Uber, Airbnb e Netflix.
Vou guiá-lo passo a passo sobre como usar o XGBoost para tarefas de regressão em Python.
Você aprenderá sobre as diferentes funções objetivo que pode usar, como avaliar seu modelo e até como plotar seus resultados.
Ao final deste tutorial, você terá uma nova ferramenta em sua caixa de ferramentas de machine learning que poderá ajudar a melhorar o desempenho do seu modelo.
Fórmulas das Funções Objetivo (Perda) para Regressão
O XGBoost oferece várias funções objetivo para tarefas de regressão.
Você pode seguir as diretrizes baseadas na teoria da probabilidade para escolher a mais adequada para o seu problema, ou testar as que acredita serem mais adequadas e comparar os resultados em um conjunto de validação (que é minha maneira favorita).
reg:squarederror
Também conhecida como Erro Quadrático Médio (L2), esta é a função objetivo padrão usada na regressão linear.
Ela minimiza a média das diferenças quadradas entre os valores previstos (y_pred) e os valores reais (y_true).
A fórmula é a seguinte:
$$L(y_{\text{true}}, y_{\text{pred}}) = (y_{\text{true}} - y_{\text{pred}})^2$$
Esta função deve ser usada quando seus dados têm distribuição normal e não há outliers significativos, ou quando você se preocupa com valores extremos, já que o erro quadrático pode ser significativamente influenciado por eles.
reg:squaredlogerror
Esta função é semelhante ao erro quadrático, mas com um ajuste logarítmico.
É útil quando o erro relativo é mais importante que o erro absoluto.
A fórmula é a seguinte:
$$L(y_{\text{true}}, y_{\text{pred}}) = (\log(y_{\text{true}} + 1) - \log(y_{\text{pred}} + 1))^2$$
Por exemplo, se você está prevendo o número de visualizações de um vídeo do YouTube, um erro de 100 visualizações é mais significativo para um vídeo com 1000 visualizações do que para um vídeo com 1 milhão de visualizações.
Esta função penalizará mais o erro do primeiro vídeo do que o do segundo.
reg:absoluteerror
Este é o erro absoluto (L1), que é a soma das diferenças absolutas entre os valores previstos e reais.
A fórmula é a seguinte:
$$ L(y_{\text{true}}, y_{\text{pred}}) = |y_{\text{true}} - y_{\text{pred}}| $$
Esta função objetivo é menos sensível a outliers comparada ao erro quadrático.
reg:pseudohubererror
A função de perda Pseudo-Huber é uma aproximação suavizada da perda de Huber, que é uma função de perda usada em regressão robusta, como o erro absoluto.
Foi desenvolvida na tentativa de combinar as vantagens das funções de perda de erro quadrático e erro absoluto.
A fórmula é a seguinte:
$$L(y_{\text{true}}, y_{\text{pred}}) = \delta^2 * (\sqrt{1 + \left(\frac{y_{\text{true}} - y_{\text{pred}}}{\delta}\right)^2} - 1)$$
Aqui, delta é um hiperparâmetro ajustável que controla o equilíbrio entre os efeitos de perda L1 e L2.
reg:gamma e reg:tweedie
As funções objetivo Gamma e Tweedie são frequentemente utilizadas nos campos de seguros e finanças.
A função objetivo reg:gamma é usada para regressão Gamma.
A distribuição Gamma é uma família de distribuições de probabilidade contínuas com dois parâmetros.
É útil quando a variável alvo é estritamente positiva e a variância é proporcional ao quadrado da média.
Isso a torna bem adequada para modelar quantidades que são valores ou tamanhos, como sinistros de seguros, quantidades de chuva ou uso de serviços.
A função objetivo reg:tweedie é usada para regressão Tweedie.
A distribuição Tweedie é um caso especial do modelo de dispersão exponencial (EDM) e inclui várias distribuições como casos especiais, como as distribuições normal, Poisson, gama e gaussiana inversa.
Isso a torna altamente flexível e capaz de modelar uma variedade de diferentes tipos de dados.
Em particular, é útil quando os dados contêm tanto um componente discreto (por exemplo, contagens zero ou inteiros positivos) quanto um componente contínuo (por exemplo, números reais positivos).
Isso a torna adequada para modelar quantidades como sinistros de seguros, onde pode haver um grande número de sinistros zero (discreto) e o tamanho do sinistro (contínuo) pode variar amplamente.
reg:quantileerror
A função objetivo de regressão quantílica (ou perda pinball) é usada quando estamos interessados em prever um intervalo (quantil) em vez de um ponto específico.
Ela é particularmente útil quando os dados têm uma distribuição assimétrica ou quando os outliers precisam ser tratados com cuidado.
A fórmula para esta função de perda para um dado quantil q é a seguinte:
Se o valor real for maior que o valor previsto (y_true > y_pred), a fórmula é:
$$L(y_{\text{true}}, y_{\text{pred}}) = q * (y_{\text{true}} - y_{\text{pred}})$$
Se o valor real for menor ou igual ao valor previsto (y_true <= y_pred), a fórmula é:
$$L(y_{\text{true}}, y_{\text{pred}}) = (1 - q) * (y_{\text{pred}} - y_{\text{true}}) $$
Aqui, q é o quantil sendo considerado (um valor entre 0 e 1).
Por exemplo, se q é 0,5, estamos considerando a mediana, e a perda Pinball se torna equivalente ao erro absoluto.
Esta função é útil quando o custo de superestimação e subestimação não são os mesmos.
Regressão XGBoost usando a API Scikit-Learn
Vamos ver um exemplo de como usar o XGBoost para tarefas de regressão usando a API Scikit-Learn.
Usaremos o conjunto de dados Wine Quality do UCI Machine Learning Repository.
Este conjunto de dados contém features químicas medidas de vinhos tintos (álcool, pH, ácido cítrico, etc.) e uma pontuação de qualidade entre 3 e 8. Quanto maior, melhor.
Nosso objetivo é treinar um modelo que possa prever a pontuação de qualidade de um vinho dadas suas features químicas.
Primeiro, precisamos importar as bibliotecas necessárias.
Usaremos pandas para manipulação de dados, XGBRegressor para nosso modelo e train_test_split do sklearn para dividir nossos dados em conjuntos de treinamento e teste.
XGBRegressor é a interface de regressão para XGBoost ao usar esta API.
import pandas as pd
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
Em seguida, carregaremos o conjunto de dados Wine Quality. Usaremos a função read_csv do pandas para fazer isso.
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = pd.read_csv(url, sep=";")
Agora, vamos dividir nossos dados em features (X) e alvo (y).
O alvo, o que queremos prever, é a coluna ‘quality’.
X = data.drop('quality', axis=1)
y = data['quality']
Dividiremos nossos dados em conjuntos de treinamento e teste.
Isso nos permite avaliar o quão bem nosso modelo generaliza para dados não vistos.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
Agora, estamos prontos para criar nosso modelo de regressão XGBoost.
Primeiro, instanciamos a classe XGBRegressor e a armazenamos em uma variável chamada model.
Vamos manter os hiperparâmetros padrão por enquanto, mas fique à vontade para ajustá-los para obter melhores resultados.
model = XGBRegressor(objective='reg:squarederror', random_state=123)
Em seguida, treinaremos nosso modelo usando o método fit.
Passamos nossos dados de treinamento e rótulos.
model.fit(X_train, y_train)
Finalmente, podemos usar nosso modelo treinado para fazer previsões em nossos dados de teste.
predictions = model.predict(X_test)
E pronto! Você acabou de treinar um modelo de regressão XGBoost usando a API Scikit-Learn.
Regressão XGBoost usando a API Nativa
Agora, vamos ver um exemplo de como usar o XGBoost para tarefas de regressão usando a API nativa.
Continuaremos usando o conjunto de dados Wine Quality do UCI Machine Learning Repository.
Desta vez, importamos objetos do módulo “raw” xgboost para construir nosso modelo.
import pandas as pd
from xgboost import DMatrix, train
from sklearn.model_selection import train_test_split
Em seguida, carregaremos o conjunto de dados Wine Quality. Usaremos a função read_csv do pandas para fazer isso.
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
data = pd.read_csv(url, sep=";")
Agora, vamos dividir nossos dados em features (X) e alvo (y).
O alvo, o que queremos prever, é a coluna ‘quality’.
X = data.drop('quality', axis=1)
y = data['quality']
Dividiremos nossos dados em conjuntos de treinamento e teste.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
Agora, estamos prontos para criar nossos objetos DMatrix.
DMatrix é uma estrutura de dados única do XGBoost que proporciona vários benefícios, incluindo velocidade e eficiência.
Ela é necessária para treinar um modelo usando a API nativa.
dtrain = DMatrix(X_train, label=y_train)
dtest = DMatrix(X_test)
Em seguida, configuraremos nossos hiperparâmetros.
Usaremos a função objetivo 'reg:squarederror' e uma taxa de aprendizado de 0,1.
params = {'objective':'reg:squarederror', 'learning_rate':0.1}
Agora, podemos treinar nosso modelo usando a função train.
Passamos nossos hiperparâmetros, dados de treinamento e o número de rodadas de boosting (também conhecido como número de árvores se estivermos usando o modelo baseado em árvores).
model = train(params, dtrain, num_boost_round=100)
Finalmente, podemos usar nosso modelo treinado para fazer previsões em nossos dados de teste.
predictions = model.predict(dtest)
E é isso! Você acabou de treinar um modelo de regressão XGBoost usando a API nativa.
Como Avaliar Modelos de Regressão XGBoost
Após treinar seu modelo e fazer previsões, você pode usar as métricas do Scikit-Learn para avalia-lo.
Para regressão, as métricas comuns incluem Erro Médio Absoluto (MAE), Erro Quadrático Médio (MSE) e Raiz do Erro Quadrático Médio (RMSE).
Veja como você pode calcular essas métricas:
from sklearn.metrics import mean_absolute_error, mean_squared_error
# Calcular MAE
mae = mean_absolute_error(y_test, predictions)
print('Erro Médio Absoluto:', mae)
# Calcular MSE
mse = mean_squared_error(y_test, predictions)
print('Erro Quadrático Médio:', mse)
# Calcular RMSE
rmse = mean_squared_error(y_test, predictions, squared=False)
print('Raiz do Erro Quadrático Médio:', rmse)
Ao usar a API nativa, você pode usar o parâmetro evals da função train para avaliar seu modelo durante o treinamento:
# Definir dados de avaliação
eval_data = [(dtrain, 'train'), (dtest, 'eval')]
# Treinar o modelo
model = train(params, dtrain, num_boost_round=100, evals=eval_data)
Isso imprimirá os erros de treinamento e avaliação em cada rodada de boosting.
Você também pode avaliar seu modelo após o treinamento usando o método eval:
# Calcular o erro
error = model.eval(dtest)
print('Erro de Avaliação:', error)
Note que o método eval requer um DMatrix com informações de rótulo.
Se você tem um novo conjunto de dados, ou não converteu seus dados de teste para um DMatrix com rótulos, você pode fazer isso da seguinte maneira:
dtest = DMatrix(X_test, label=y_test)
Lembre-se, o objetivo é tornar seu erro o menor possível.
Se o desempenho do seu modelo não for satisfatório, você pode precisar ajustar seus parâmetros, coletar mais dados ou tentar uma abordagem diferente.
Como Plotar Resultados de Regressão XGBoost
Plotar seus resultados de regressão é uma ótima maneira de entender visualmente o desempenho do seu modelo.
Primeiro, vamos começar plotando os valores reais contra os valores previstos. Um modelo perfeito resultaria em uma linha reta onde y_true = y_pred.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 5))
plt.scatter(y_test, predictions)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], color='red', linewidth=2)
plt.xlabel('Valores Reais')
plt.ylabel('Valores Previstos')
plt.title('Valores Reais vs Valores Previstos')
plt.show()
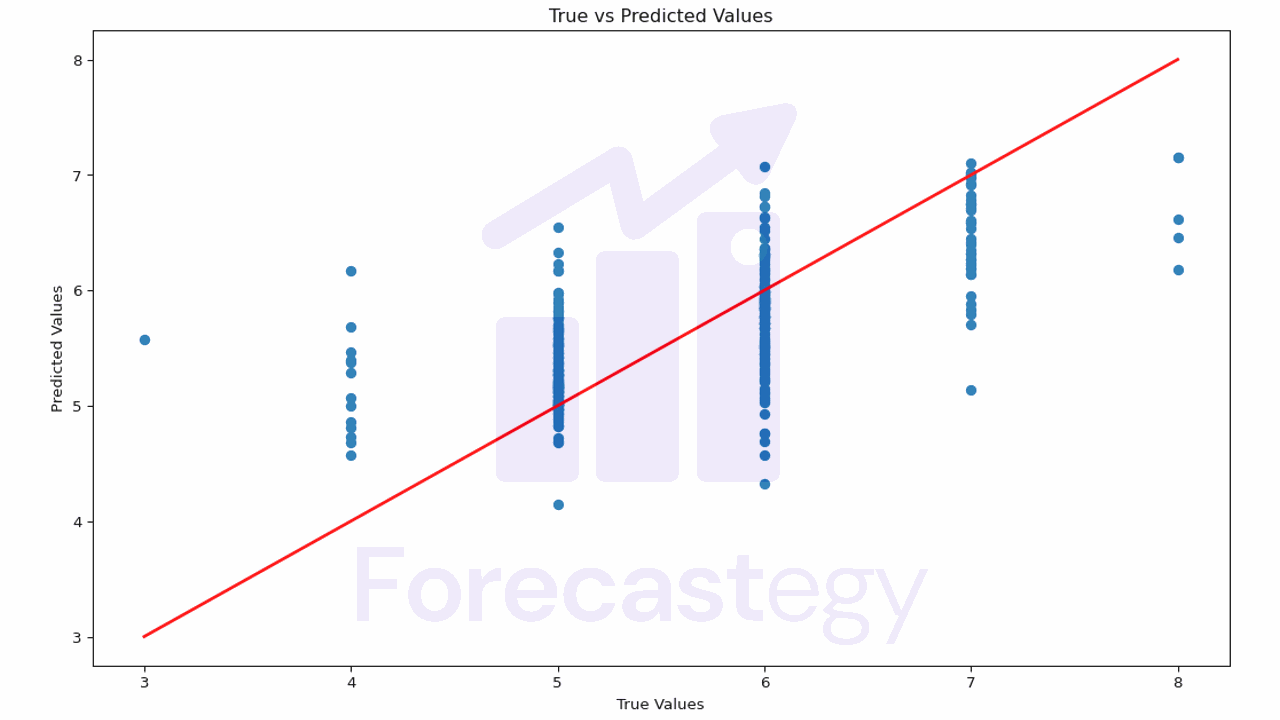
Este gráfico ajuda você a entender o quão próximas as previsões estão dos valores reais.
Se os pontos estiverem muito dispersos da linha vermelha, significa que as previsões do modelo não são muito precisas.
No nosso caso, é mais difícil avaliar, porque nossos valores reais são discretos (3, 4, 5, 6, 7, 8) e nossas previsões são contínuas.
Podemos usar a função de gráfico de violino do Seaborn para ter uma visão mais clara da distribuição dos valores previstos para cada valor real.
O gráfico de violino combina um box plot com um gráfico de densidade do kernel, o que pode nos dar mais informações sobre a distribuição dos valores.
import seaborn as sns
plt.figure(figsize=(10, 5))
sns.violinplot(x=y_test, y=predictions)
plt.xlabel('Valores Reais')
plt.ylabel('Valores Previstos')
plt.title('Gráfico de Violino dos Valores Previstos para Cada Valor Real')
plt.show()
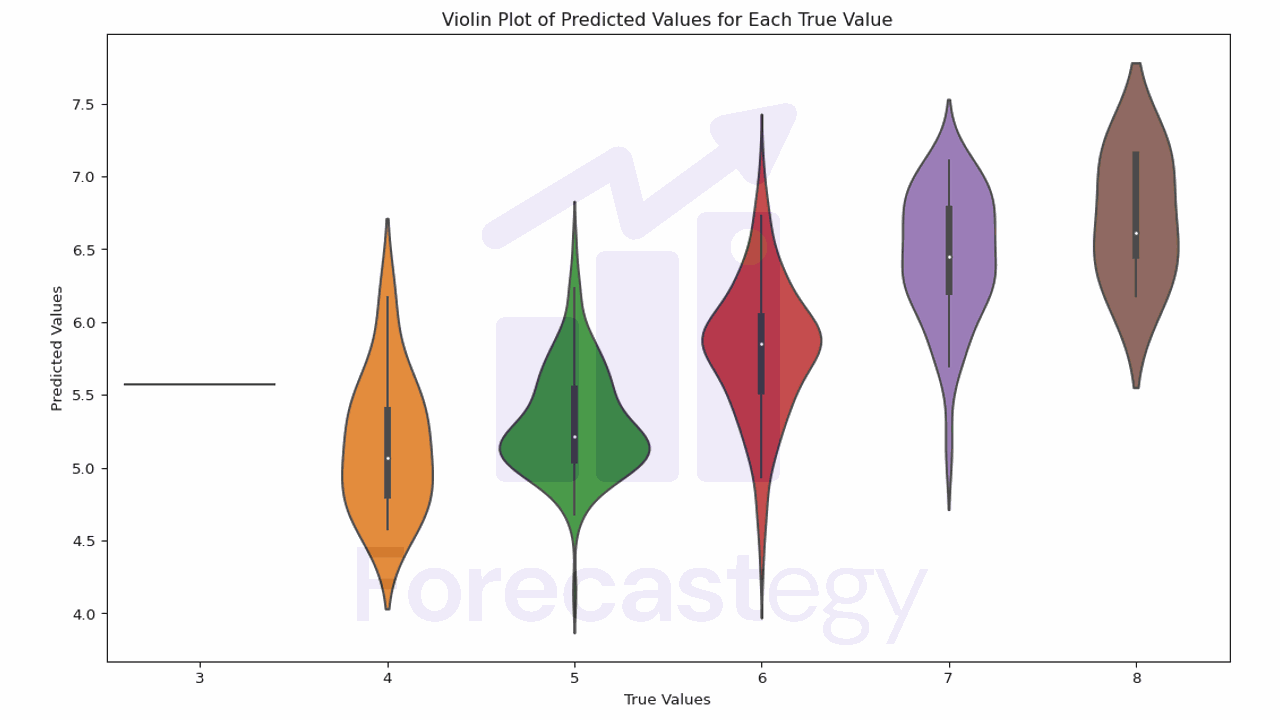
Neste gráfico, a largura do violino representa a densidade dos dados.
O ponto branco é a mediana, e a caixa representa o intervalo interquartil (IQR). As linhas são 1,5 vezes o IQR.
Idealmente, a massa de cada violino deve estar centralizada no valor real.
Vemos que, para vinhos de qualidade 4, o modelo tende a superestimar a qualidade.
Ele é melhor em 5 e 6, e tende a subestimar a qualidade para 7 e 8.
Outro gráfico útil é a distribuição dos resíduos (a diferença entre os valores reais e os valores previstos).
Um bom modelo teria resíduos centrados em 0 e distribuídos de acordo com uma distribuição normal.
residuos = y_test - predictions
plt.figure(figsize=(10, 5))
plt.hist(residuos, bins=20)
plt.xlabel('Resíduo')
plt.ylabel('Frequência')
plt.title('Distribuição dos Resíduos')
plt.show()
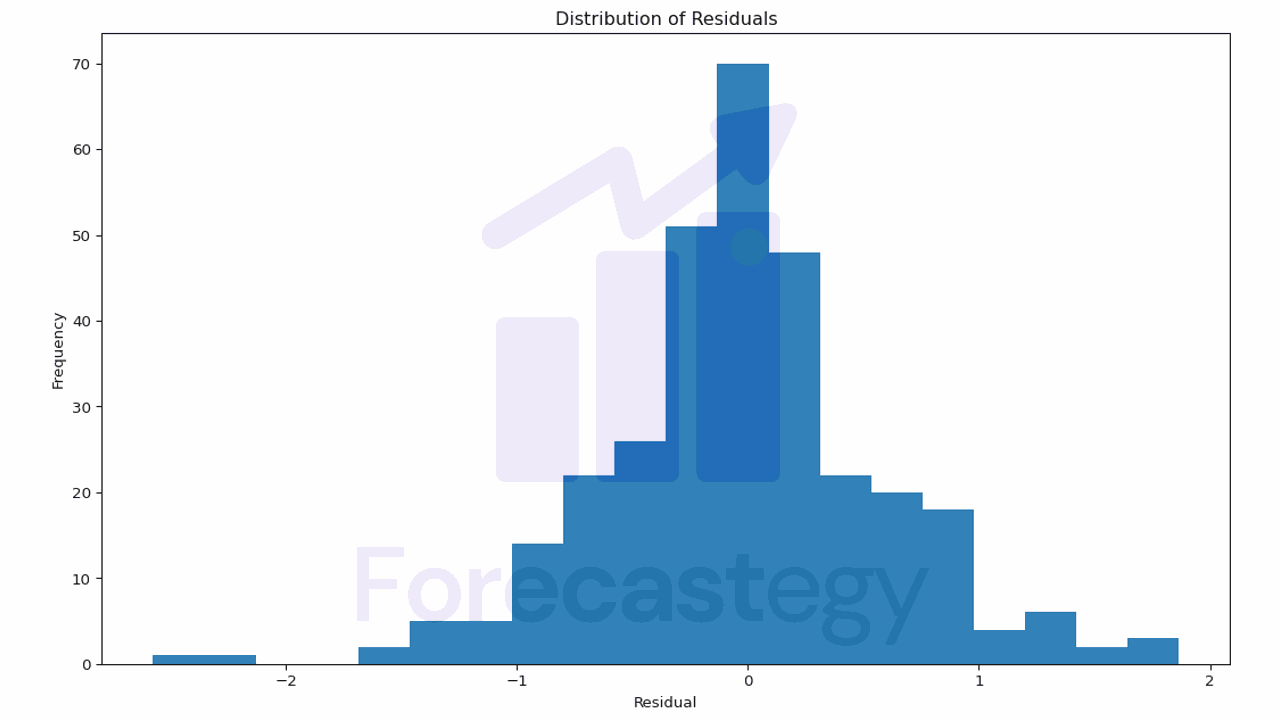
Se os resíduos não estiverem centrados em 0 ou tiverem uma distribuição assimétrica, pode indicar que seu modelo está sistematicamente superestimando ou subestimando a variável alvo.
No nosso caso, o modelo parece bom.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.