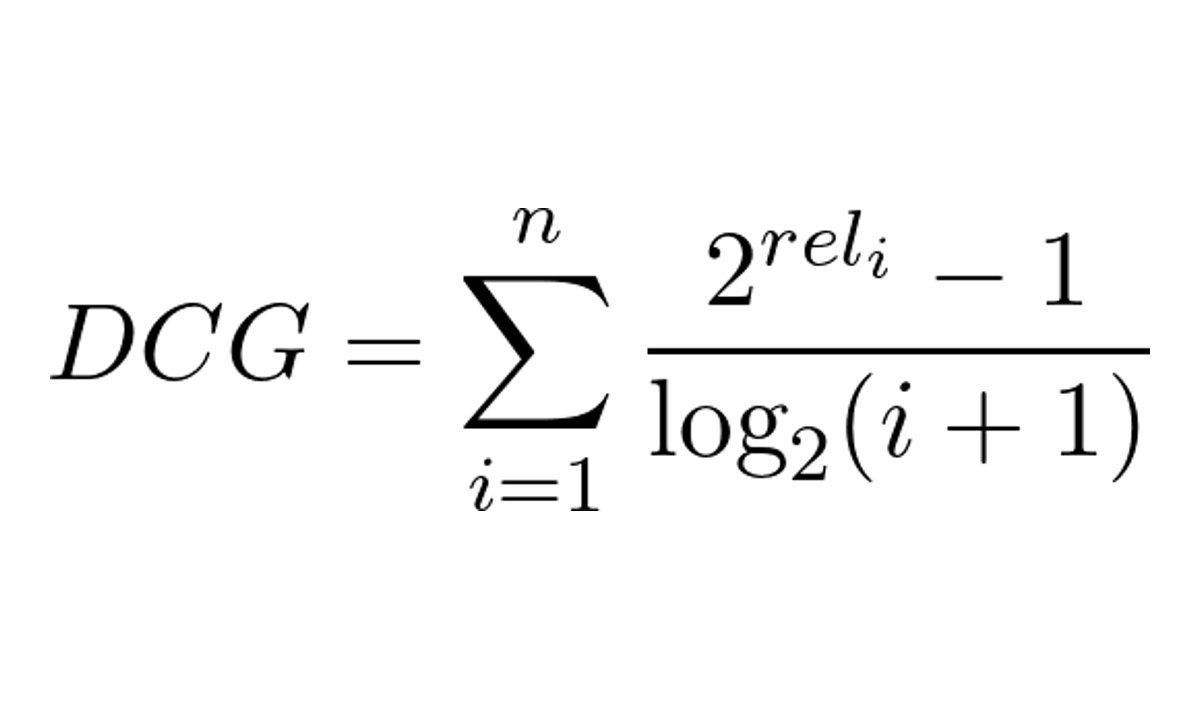Índice
- O Que é NDCG?
- Como Interpretar o NDCG?
- Qual a Fórmula do NDCG?
- Como Calcular o NDCG em Python?
- Qual a Diferença Entre NDCG e Mean Average Precision?
- Qual a Diferença Entre NDCG e Mean Reciprocal Rank?
O Que é NDCG?
O NDCG é uma métrica de avaliação de desempenho que é especialmente útil para modelos de machine learning de ranking.
Ela é muito usada em sistemas de busca e recomendação. Eu mesmo a usava para avaliar os sistemas de ranking de freelancers quando trabalhei na Upwork.
Ele mede a qualidade de uma lista de resultados retornada pelo modelo em relação aos itens que o usuário realmente indicou como relevantes.
O “Normalized” no nome se refere ao fato do NDCG ser o Discounted Cumulative Gain (DCG) dos resultados previstos dividido pelo “Ideal DCG” (IDCG) que seria a lista de resultados perfeita.
Isso facilita a comparação entre diferentes modelos de machine learning.
Você vai entender melhor o que tudo isso significa depois de ler este artigo.
Uma das maiores vantagens desta métrica é que ela leva em conta a posição dos resultados relevantes na lista.
Isso significa que um resultado relevante que aparece no topo da lista terá uma pontuação mais alta do que se ele aparecesse no final.
A desvantagem é a dificuldade em calcular e interpretar a fórmula.
Como Interpretar o NDCG?
Primeiro precisamos entender o Discounted Cumulative Gain (DCG) que é a parte mais importante do NDCG.
Ele é calculado atribuindo pontos aos resultados relevantes de acordo com a relevância e a posição deles na lista.
A fórmula do DCG para uma lista de resultados é:
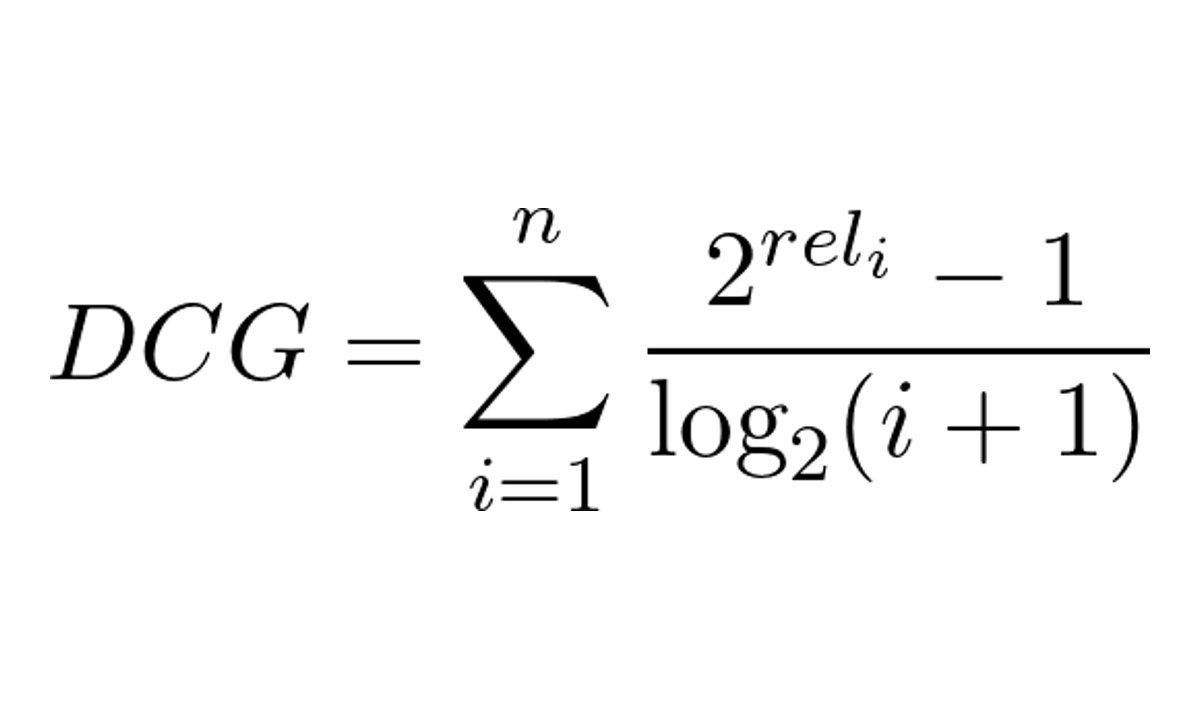
Onde:
- n é o número de resultados na lista (podemos pensar como itens recomendados ao usuário)
- i é a posição do item na lista
- rel_i é a relevância do item i (por exemplo, qual nota o usuário deu a um produto)
Vamos ver um exemplo de como calcular o DCG para uma lista de resultados.
| Posição | ID do Item | Relevância | 2^rel_i - 1 | log2(i+1) | DCG Posição |
|---|---|---|---|---|---|
| 1 | A | 2 | 3 | 1 | 3 |
| 2 | B | 3 | 7 | 1.58496 | 4.41651 |
| 3 | C | 0 | 0 | 2 | 0 |
| 4 | D | 1 | 1 | 2.32193 | 0.430677 |
| 5 | E | 2 | 3 | 2.58496 | 1.16056 |
Considere que este é o resultado de um modelo de machine learning de recomendação, mas o mesmo vale para qualquer modelo que precise ordenar uma lista.
A coluna “Posição” é a posição do item na lista retornada, sendo 1 para o primeiro item e 5 para o último.
A coluna “ID do Item” é o ID do item recomendado, que poderia ser um filme, música, livro, vídeo, etc.
A coluna “Relevância” é a relevância do item para o usuário. Para treinar e validar o modelo isso pode ser calculado com base nos dados históricos considerando interações do usuário com itens como cliques, compras, tempo de visualização, etc.
O item mais relevante para esse usuário é o B, com relevância 3, seguido pelos itens A e E com relevância 2 e D com relevância 1. O item C é irrelevante.
A relevância pode ser um valor binário, como 0 ou 1, ou um valor numérico, como 0, 1, 2, 3, etc. E podem ter empates como no caso dos itens A e E no exemplo acima.
A coluna “2^rel_i - 1” é numerador do DCG: o valor de 2 elevado à relevância do item menos 1.
Isso significa que cada ponto de relevância traz ganhos exponenciais.
Um item com relevância 1 vale 2^1 - 1 = 1 ponto, um item com relevância 2 vale 2^2 - 1 = 3 pontos, um item com relevância 3 vale 2^3 - 1 = 7 pontos, e assim vai.
A coluna “log2(i+1)” é o denominador do DCG: o logaritmo na base 2 da posição do item na lista mais 1.
Isso significa que quanto mais baixa a posição do item na lista, maior será a penalidade sobre a relevância no cálculo do DCG, mas numa escala logarítmica.
A importância diminui exponencialmente conforme os resultados vão ficando para trás.
Isso reflete a ideia de que os primeiros resultados são mais importantes que os seguintes.
A coluna “DCG Posição” mostra o cálculo dessa fração para cada item.
Nós temos um ganho bom com os dois primeiros itens, mas veja como apesar da relevância do item B ser maior, o ganho acaba penalizado por estar na segunda posição.
Enquanto o item C, irrelevante, zera o ganho que poderíamos ter na terceira posição.
Para obter o DCG desta lista, basta somar os valores de cada item, que dá um total aproximado de 9,01.
Se pararmos por aqui, o DCG seria uma métrica útil mas difícil de comparar e interpretar, já que ele não tem uma escala específica e depende do número de itens na lista.
Vamos ver então como normalizar o DCG para facilitar a interpretação e comparação.
Qual a Fórmula do NDCG?
O NDCG é o DCG dos resultados normalizado pelo DCG ideal.
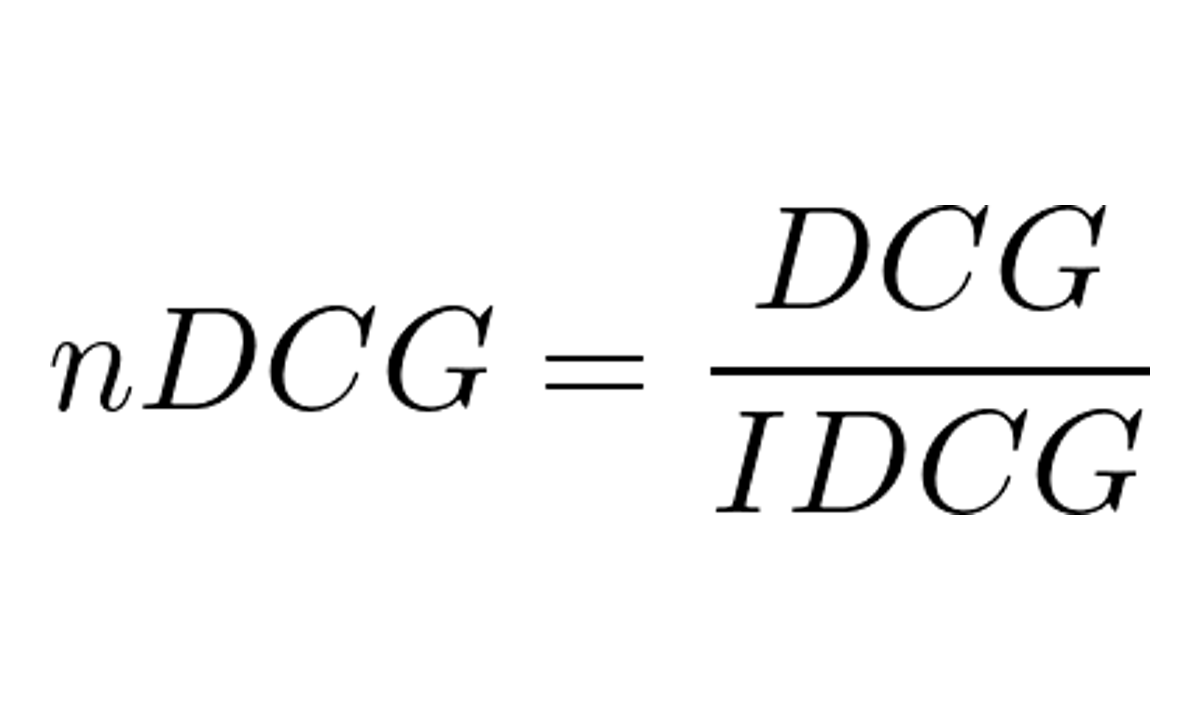
Onde:
- DCG é o DCG dos resultados como calculado acima
- IDCG é o DCG ideal, que é o DCG dos resultados ordenados por relevância (a lista perfeita)
Para calcular o IDCG, vamos ordenar os resultados por relevância e calcular o DCG como fizemos acima.
| Posição | ID do Item | Relevância | 2^rel_i - 1 | log2(i+1) | DCG Posição |
|---|---|---|---|---|---|
| 1 | B | 3 | 7 | 1 | 7 |
| 2 | A | 2 | 3 | 1.58496 | 1.89279 |
| 3 | E | 2 | 3 | 2 | 1.5 |
| 4 | D | 1 | 1 | 2.32193 | 0.430677 |
| 5 | C | 0 | 0 | 2.58496 | 0 |
Veja que agora o item B é o melhor posicionado, seguido pelos itens A e E, e assim por diante.
Ao somar o DCG de cada item, temos um total aproximado de 10,82 que é o IDCG ou DCG ideal.
Esta é a pontuação máxima que o modelo poderia ter alcançado se ordenasse os itens perfeitamente.
Com estes dois números, basta dividir o DCG pelo IDCG para obter o NDCG. Um valor entre 0 e 1, sendo que quanto mais próximo de 1, melhor.
Neste caso, seria de aproximadamente 0,83. Muito bom!
Agora basta calcular o NDCG para cada lista de resultados e calcular a média para obter o NDCG do seu modelo em todo o conjunto de dados.
Como Calcular o NDCG em Python?
Apesar do scikit-learn ter uma função para calcular o NDCG, ela faz o cálculo com uma fórmula diferente da mostrada acima, que é utilizada pela maior parte da indústria e competições de machine learning.
Em vez de considerar 2 elevado à relevância menos 1, ela considera apenas a relevância bruta no numerador.
Então, vou te mostrar como calcular esta versão com mais peso para a relevância usando Numpy:
import numpy as np
y_pred_rel = np.array([[2,3,0,1,2],
[1,2,1,1,0],
[3,3,2,1,1]])
positions = np.arange(1, y_pred_rel.shape[1]+1)
denominator = np.log2(positions+1)
dcg = np.sum((2**y_pred_rel - 1) / denominator,axis=1)
ideal_rel = np.sort(y_pred_rel, axis=1)[:,::-1]
idcg = np.sum((2**ideal_rel - 1) / denominator, axis=1)
ndcg = dcg / idcg
print(ndcg.mean())
Neste caso imagine que temos uma matriz de resultados para três usuários, com cinco itens em cada lista.
Os valores da matriz y_pred_rel são as relevâncias dos itens recomendados naquela posição para cada usuário.
Por exemplo, para o primeiro usuário (primeira linha), são os mesmos valores do exemplo na explicação da fórmula do DCG: o item na primeira posição tem relevância 2, o segundo item tem relevância 3, e assim por diante.
Na segunda linha já temos outra lista de resultados, com os itens recomendados para o segundo usuário.
Na prática é comum que você calcule o NDCG sobre uma lista de listas de resultados, que pode ser facilmente organizada na mesma forma da matriz acima.
Para deixar os cálculos mais rápidos, vamos criar o vetor denominator com o log2 aplicado às posições de cada item mais 1.
Este vetor é o mesmo para todos os usuários, já que todas as listas têm o mesmo número de itens.
O Numpy faz o broadcast automático para que possamos dividir a matriz y_pred_rel, após a transformação no numerador, pelo vetor denominator.
Isso significa que mesmo passando uma matriz para divisão por um vetor, o vetor é replicado para cada linha da matriz internamente.
Fazendo a soma com axis=1, temos o DCG para cada linha da matriz, ou seja, para cada lista de resultados.
Agora vamos criar a matriz ideal_rel com os itens ordenados por relevância, do mais relevante para o menos relevante.
Para isso, vamos usar a função np.sort com o argumento axis=1 para ordenar cada linha da matriz de maneira ascendente, e o argumento ::-1 para inverter a ordem.
Depois disso é só repetir o processo de cálculo do DCG com a matriz ideal_rel para obter o IDCG de cada lista.
Por fim, basta dividir o DCG pelo IDCG para obter o NDCG de cada usuário, e calcular a média para obter o NDCG do seu modelo.
Qual a Diferença Entre NDCG e Mean Average Precision?
Essas duas métricas são muito similares, mas existem duas diferenças principais que você deve levar em consideração:
O NDCG é mais difícil de interpretar do que a MAP.
Basta você olhar a fórmula explicada lá em cima e perceber que é muito mais difícil entender como o equilíbrio entre a relevância dos itens e a posição deles na lista afeta a pontuação.
A MAP é muito mais fácil de calcular e entender, já que é similar a uma média da precisão em cada posição da lista.
O MAP não leva em conta a magnitude da relevância dos itens.
Ela é uma métrica baseada em precisão, o que significa que ela não se importa se o item 1 é 10 vezes mais relevante que o item 2.
Se a relevância dos itens é binária, pode ser melhor usar o MAP por causa da interpretabilidade.
Caso não, o NDCG pode ser melhor, já que ele leva em conta a magnitude da relevância.
Uma observação adicional: existem muitas maneiras de manipular a fórmula do NDCG para ajustar a transformação da relevância e a penalidade da posição.
Em casos mais complexos, isso pode ser uma vantagem, já que ajustar a fórmula pode fazê-la correlacionar melhor com melhorias em métricas de negócio durante o teste em produção.
No nosso exemplo, este seriam os valores da Average Precision para cada posição, considerando que um item é relevante se a relevância for maior que 0:
| Posição | ID do Item | Relevância | DCG Posição | Average Precision |
|---|---|---|---|---|
| 1 | A | 2 | 3 | 1 |
| 2 | B | 3 | 4.41651 | 1 |
| 3 | C | 0 | 0 | 0 |
| 4 | D | 1 | 0.430677 | 0.75 |
| 5 | E | 2 | 1.16056 | 0.8 |
Na primeira posição temos 1 item relevante de 1 possível, o que dá uma precisão de 1.
Na segunda posição temos 2 itens relevantes de 2 possíveis, que também dá uma precisão de 1.
Na terceira posição temos 2 itens relevantes de 3 possíveis, mas como o item na terceira posição não é relevante, substituímos a precisão por 0.
Na quarta posição temos 3 itens relevantes de 4 possíveis, e como o item é relevante, a precisão é 3/4 = 0,75.
Como você pode ver, a MAP não levou em conta que o item da segunda posição é mais relevante que o item da primeira posição e deu o mesmo score para ambos. Já o DCG conseguiu diferenciar.
No fim, somamos todas as precisões e dividimos pelo número máximo possível de itens relevantes.
Esse número é de, pelo menos, quatro, já que temos 4 itens relevantes na lista mas podem haver outros que não foram retornados entre os 5 primeiros.
Qual a Diferença Entre NDCG e Mean Reciprocal Rank?
Expliquei a diferença entre Mean Reciprocal Rank e NDCG neste post.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.