Índice
- O Que é Mean Reciprocal Rank?
- Qual a Fórmula do Mean Reciprocal Rank?
- Como Interpretar o Mean Reciprocal Rank?
- Como Calcular o Mean Reciprocal Rank em Python?
- Qual a Diferença Entre Mean Reciprocal Rank e NDCG?
- Qual a Diferença Entre Mean Reciprocal Rank e Mean Average Precision?
O Que é Mean Reciprocal Rank?
O Mean Reciprocal Rank (MRR) é uma métrica comumente utilizada para avaliar a qualidade de modelos de machine learning que retornam uma lista de resultados relevantes.
Ela é uma métrica robusta a diferentes tamanhos de listas de recomendação, ou seja, é independente do tamanho da lista.
O MRR também é robusto a diferentes tamanhos de conjuntos de itens recomendados corretos, pois ele só se preocupa com o item relevante mais bem rankeado.
Isso pode ser um problema, pois os resultados podem conter muitos itens irrelevantes e isso não afetará negativamente a pontuação MRR, desde que haja algum item relevante no início da lista.
Em termos de experiência de usuário isso é péssimo. Imagine ter apenas um item relevante no topo de uma lista de dez itens.
Por isso, no fim do artigo vou discutir a diferença dela com outras métricas, como NDCG e MAP.
Vou usar o exemplo de recomendação de itens para usuários para ilustrar o MRR no artigo, mas outro caso de uso seria imaginar que cada “usuário” é um termo de pesquisa num site e as listas de recomendações são os resultados da busca.
Qual a Fórmula do Mean Reciprocal Rank?
A fórmula do MRR é dada por:
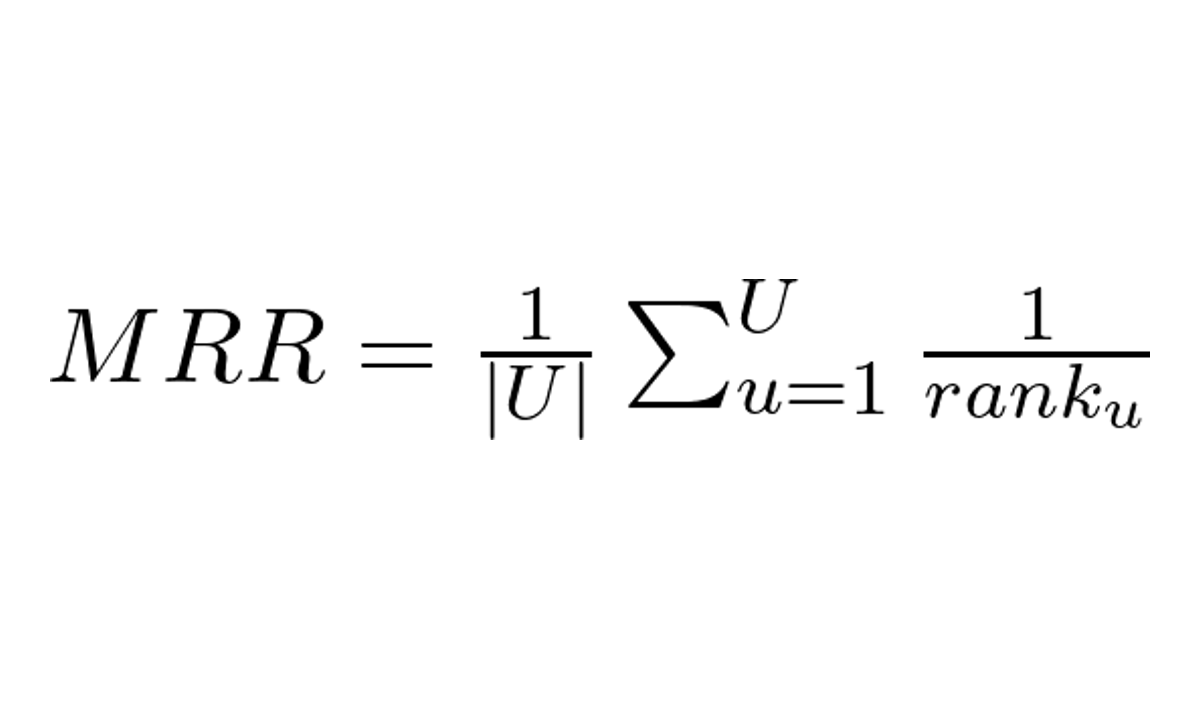
Onde:
- U é o número de usuários (ou listas de recomendações, resultados)
- rank_u é a posição do primeiro item relevante na lista de recomendações do usuário u
Primeiro criamos uma lista de recomendações para cada usuário.
Essas recomendações devem ser ordenadas de acordo com relevância prevista de cada item. Itens mais relevantes primeiro.
Essa lista pode ter previsões de relevância diferentes para cada item ou ser simplesmente um indicador binário.
Depois, para cada usuário, percorremos a lista e calculamos o inverso multiplicativo da posição do primeiro item relevante (o “reciprocal rank”).
Por fim, calculamos a média desses valores levando em conta todos os usuários.
Caso não haja itens relevantes numa lista de resultados, substituímos o valor do reciprocal rank por zero.
Como Interpretar o Mean Reciprocal Rank?
O Mean Reciprocal Rank vai de 0 a 1. Quanto mais próximo de 1, melhor.
Um valor igual a um significa que todos os itens na primeira posição de cada lista são relevantes.
Um valor igual a zero significa que nenhum item relevante está nas listas de resultados.
Na maioria dos casos o MRR ficará entre zero e um. Existem duas razões principais para isso que você pode investigar:
- O sistema de recomendação está retornando itens relevantes, mas em posições maiores que os itens irrelevantes.
- O sistema de recomendação está tendo dificuldade em identificar itens relevantes para alguns usuários, fazendo com que algumas listas tenham apenas itens irrelevantes.
Em qualquer destes casos, supondo que os dados estejam corretos, você pode melhorar a solução com a caixa de ferramentas típica de machine learning: testar outros modelos, features, dados, ajuste de hiperparâmetros, etc.
Como Calcular o Mean Reciprocal Rank em Python?
Infelizmente não temos uma função para fazer esse cálculo facilmente usando o scikit-learn.
Mas vamos implementar uma versão simples em Python puro e entender o código passo-a-passo:
recommendation_lists = [ [1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]]
relevance_lists = [ [2],
[5, 6],
[11]]
mrr = 0
for user_rel, user_rec in zip(relevance_lists, recommendation_lists):
for i, item in enumerate(user_rec):
if item in user_rel:
mrr += 1 / (i + 1)
break
mrr = mrr / len(recommendation_lists)
print(mrr)
Temos a recommendation_lists que é uma lista com as listas de recomendações para cada usuário.
Neste caso vamos recomendar apenas 4 itens para cada um.
Para o primeiro, recomendamos os itens [1, 2, 3, 4].
Na variável relevance_lists temos a lista de itens relevantes para cada usuário.
Esta é a lista de itens que sabemos ser relevantes para cada um.
Mas não é isso que queremos prever? Claro, mas para treinar e validar o modelo vamos extrair itens que o usuário tenha indicado como relevante para ele em suas interações com a empresa.
Podem ser itens que foram comprados, clicados, lidos, avaliados positivamente, etc. Isso depende do caso de uso.
Para o primeiro usuário, temos apenas o item [2] como relevante.
Agora vamos percorrer as listas de recomendações e de itens relevantes e calcular o MRR.
Para cada usuário, considerando que os itens estão ordenados de acordo com a relevância prevista, do mais relevante para o menos relevante, vamos verificar se cada item está na lista de itens relevantes até acharmos algum que esteja.
Quando encontramos um item relevante, calculamos o inverso multiplicativo, ou reciprocal rank, 1 / rank(i+1) e somamos ao MRR.
O i+1 é necessário porque a posição do primeiro item em Python é zero mas queremos começar do número um.
Note que ao encontrar o item relevante, interrompemos o loop e passamos para o próximo usuário.
Se não encontrarmos nenhum item relevante na lista de recomendações, não fazemos nada, que dá na mesma de considerar o reciprocal rank como zero.
Por fim, dividimos a soma desses reciprocal ranks pelo número de usuários para obter o MRR.
Qual a Diferença Entre Mean Reciprocal Rank e NDCG?
O NDCG (Normalized Discounted Cumulative Gain) também é uma métrica de ranking, mas é mais poderosa e completa do que o MRR.
Igual ao MRR, ela vai de 0 a 1, sendo 1 o melhor valor possível.
Diferente do MRR, que se concentra apenas na posição do primeiro item relevante recomendado, o NDCG leva em conta a posição de todos os itens da lista.
Uma vantagem clara do MRR é a interpretabilidade: o MRR é mais fácil de ser explicado e calculado comparado ao NDCG.
Fazendo uma analogia dos resultados recomendados com uma prova escolar nas quais as questões mais difíceis vêm primeiro: o MRR daria a nota baseado na primeira resposta correta dada pelo aluno, enquanto o NDCG daria a nota baseado em todas as respostas.
Se a prova tiver vinte questões e o aluno acertar a segunda questão por sorte, vai ganhar nota quase máxima no MRR, mesmo que erre todo o resto da prova. Isso não acontece no NDCG.
Veja este exemplo em que o Reciprocal Rank é o mesmo para todas as amostras, mas o NDCG consegue capturar as diferenças na posição dos itens relevantes:
| Usuário | Recomendações | Itens Relevantes | Reciprocal Rank | NDCG |
|---|---|---|---|---|
| 1 | [1, 2, 3, 4] | [1, 2] | 1 | 1 |
| 2 | [1, 2, 3, 4] | [1, 3] | 1 | 0.919721 |
| 3 | [1, 2, 3, 4] | [1, 4] | 1 | 0.877215 |
Em todos os casos, o primeiro item recomendado é relevante, o que faz o MRR ser igual a 1.
Mas quando consideramos a posição dos outros itens relevantes na lista, o NDCG consegue capturar a diferença entre colocá-los numa posição mais alta ou baixa.
Caso haja apenas um item relevante a ser recomendado, o MRR é uma boa opção. Mas se houver mais de um item relevante, o NDCG é uma opção melhor.
Nos casos que estamos vendo, todos os itens possuem o mesmo grau de relevância, mas uma outra vantagem do NDCG é que ele pode ser usado para avaliar sistemas de recomendação que atribuem relevâncias diferentes de zero e um para os itens.
Qual a Diferença Entre Mean Reciprocal Rank e Mean Average Precision?
A Mean Average Precision (MAP) é outra métrica de ranking que também é usada para avaliar sistemas de recomendação.
Ela também vai de 0 a 1, sendo 1 o melhor resultado possível.
Ela não é tão completa quanto o NDCG, mas é um ponto intermediário entre ele e o MRR.
Enquanto o MRR se concentra na posição do primeiro item relevante, a MAP leva em conta a precisão média de todos os itens relevantes, tornando-a uma métrica mais completa para ter uma visão da lista toda.
O MAP vai calcular a precisão sequencialmente para cada item da lista e depois calcular a média dessas precisões.
Na nossa tabela de exemplos:
| Usuário | Recomendações | Itens Relevantes | Reciprocal Rank | NDCG | Average Precision |
|---|---|---|---|---|---|
| 1 | [1, 2, 3, 4] | [1, 2] | 1 | 1 | 1 |
| 2 | [1, 2, 3, 4] | [1, 3] | 1 | 0.919721 | 0.833333 |
| 3 | [1, 2, 3, 4] | [1, 4] | 1 | 0.877215 | 0.75 |
Ela também levou em conta a posição de todos os itens relevantes na lista, mas de uma forma mais simples e fácil de entender do que o NDCG.
Mais uma vez estamos considerando recomendações binárias, mas o NDCG será mais adequado caso haja diferença entre o grau de relevância dos itens.
Exceto no caso acima, os argumentos que foram feitos para o NDCG com relação ao MRR também se aplicam para a MAP.
Seja o primeiro a saber das novidades em Machine Learning. Me siga no LinkedIn.